Probabilidades
Num saco existem n bolas numeradas. Metade têm um número negativo e a outra metade têm um número positivo.
Retiram-se ao acaso duas bolas sem reposição.
Sejam dois acontecimentos:
A-"o produto dos dois números é positivo"
B-"o produto dos dois números é negativo"
Qual dos acontecimentos tem maior probabilidade de se verificar?
Retiram-se ao acaso duas bolas sem reposição.
Sejam dois acontecimentos:
A-"o produto dos dois números é positivo"
B-"o produto dos dois números é negativo"
Qual dos acontecimentos tem maior probabilidade de se verificar?
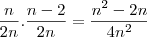
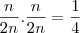
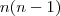 , pois a cada uma das
, pois a cada uma das 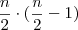
![2 \cdot \left[\frac{n}{2} \cdot (\frac{n}{2}-1)\right]=n \cdot (\frac{n}{2}-1)=\frac{n^2}{2}-n=\frac{n^2-2n}{2} 2 \cdot \left[\frac{n}{2} \cdot (\frac{n}{2}-1)\right]=n \cdot (\frac{n}{2}-1)=\frac{n^2}{2}-n=\frac{n^2-2n}{2}](/latexrender/pictures/70b6c77f8dd245696029b26d50bb88db.png)
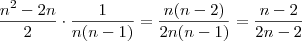
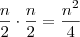
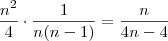
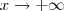 de ambas expressões cheguei a
de ambas expressões cheguei a  para o acontecimento
para o acontecimento  para o acontecimento
para o acontecimento 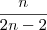
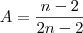
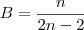
 já que o exercício é genérico.
já que o exercício é genérico. ), do que com o mesmo sinal da 1a. bola (
), do que com o mesmo sinal da 1a. bola (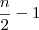 ).
).