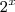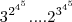A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por victoreis1 » Qui Nov 25, 2010 18:40
por victoreis1 » Qui Nov 25, 2010 18:40
Quem é maior,
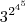
ou
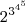
?
obs: note-se que

não consegui fazer.. se forem tentar, por favor, nem tentem calcular "quanto vale" cada número..
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por victoreis1 » Sex Nov 26, 2010 01:27
por victoreis1 » Sex Nov 26, 2010 01:27
acho que consegui.. vejam se tá certo:
seja

. Suponha que
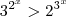
.
Usando logaritmo:

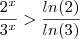
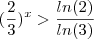
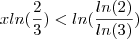
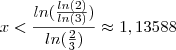
já que x =
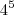
, então
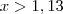
(absurdo)
logo temos que
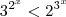
.
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Loretto » Sex Nov 26, 2010 01:29
por Loretto » Sex Nov 26, 2010 01:29
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por Rogerio Murcila » Sex Nov 26, 2010 13:24
por Rogerio Murcila » Sex Nov 26, 2010 13:24
-
Rogerio Murcila
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Sex Set 10, 2010 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eletronica / Quimica / Adm
- Andamento: formado
 por Loretto » Sex Nov 26, 2010 14:03
por Loretto » Sex Nov 26, 2010 14:03
Vamos lá.
Pergunta-se qual das potências seguintes é a maior:
[(3²)^4]^5
ou
[(2³)^4]^5
Veja que cada uma pode ser reescrita assim:
3^40
ou
2^60
Agora, para saber qual a maior, vamos aplicar logaritmo a cada uma, ficando:
log3^40 -------> 40log3
ou
log2^60 -----> 60log2
Como log3 é aproximadamente 0,4771 e log2 é aproximadamente 0,30103, vamos substituir em cada uma das expressões:
40log3 ----> 40*0,4771 = 19,084
ou
60log2 ----> 60*0,30103 = 18,062
Veja que o número formado a partir de 3^40 tem 20 algarismos (19 da característica do logaritmo + uma unidade).
E o número formado a partir de 2^60 tem 19 algarismos(18 da característica do logaritmo + 1 unidade).
Então, 3^40 é maior do que 2^60.
OK?
Adjemir.
Editado pela última vez por
Loretto em Sex Nov 26, 2010 14:08, em um total de 1 vez.
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por Loretto » Sex Nov 26, 2010 14:05
por Loretto » Sex Nov 26, 2010 14:05
Espero que ajude !
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por victoreis1 » Sex Nov 26, 2010 14:35
por victoreis1 » Sex Nov 26, 2010 14:35
tá errado loretto

-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rogerio Murcila » Sex Nov 26, 2010 15:53
por Rogerio Murcila » Sex Nov 26, 2010 15:53
Vamos lá:
Resolvendo o primeiro numero
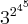
Temos ---
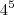
= 1024
ai fica
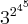
=

=
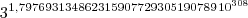

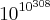
Resolvendo o segundo numero
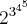
Temos ---
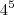
= 1024
ai fica
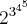
=
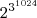
=
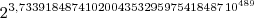


Portanto
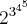
é maior que
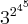
-
Rogerio Murcila
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Sex Set 10, 2010 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eletronica / Quimica / Adm
- Andamento: formado
 por 0 kelvin » Sex Nov 26, 2010 19:34
por 0 kelvin » Sex Nov 26, 2010 19:34
É, no começo achei q dava pra multiplicar os expoentes como se fosse
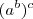
mas como tem aquela indicação que não pode fazer isso, então a conclusão q eu tinha chegado tb q era:

é falsa por potenciação feita errado.
Eu só sei fazer quando a questão dá pelo menos um log aproximado, pq aí é só fatorar.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por Loretto » Sex Nov 26, 2010 23:28
por Loretto » Sex Nov 26, 2010 23:28
Quem disse que não podi ? Num é tudo potência ? Intão podi uai !!
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por MarceloFantini » Sex Nov 26, 2010 23:37
por MarceloFantini » Sex Nov 26, 2010 23:37
Eu sinceramente espero que você esteja brincando, Loretto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Lorettto » Sáb Nov 27, 2010 01:37
por Lorettto » Sáb Nov 27, 2010 01:37
"Quem disse que não podi ? Num é tudo potência ? Intão podi uai !!"
O meu comentário acima foi para a resolução que eu postei. Ou seja, estando tudo entre parênteses, faça a minha resolução. Senão, não faça. E brincar, eu só brinco com quem eu conheço, e de preferência, amigos !

-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por victoreis1 » Sáb Nov 27, 2010 01:39
por victoreis1 » Sáb Nov 27, 2010 01:39
Mais outra, quem sabe um pouco mais difícil.
Peço-lhes novamente que resolvam logicamente/algebricamente, não tentem calcular, não tem graça ^^
Quem é maior,

ou

?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Lorettto » Sáb Nov 27, 2010 02:13
por Lorettto » Sáb Nov 27, 2010 02:13
20^{50} > 50 !
-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por 0 kelvin » Sáb Nov 27, 2010 11:44
por 0 kelvin » Sáb Nov 27, 2010 11:44
Potência de base 2, uma hora dobra e passa o fatorial, depois dobra, dobra e o fatorial fica pra trás.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por victoreis1 » Sáb Nov 27, 2010 12:25
por victoreis1 » Sáb Nov 27, 2010 12:25
Ambos estão certos, mas notem que não é tão óbvio assim. Notem que
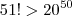
.
Alguém consegue fazer essa questão sem ser indutivamente?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por 0 kelvin » Sáb Nov 27, 2010 12:31
por 0 kelvin » Sáb Nov 27, 2010 12:31
Função?
f(x) = x!
f(x) =
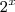
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por meuemail » Seg Dez 13, 2010 01:12
por meuemail » Seg Dez 13, 2010 01:12
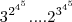
Mas isto é válido

Editado pela última vez por
meuemail em Seg Dez 13, 2010 02:04, em um total de 3 vezes.
-
meuemail
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Dez 11, 2010 23:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por Lorettto » Seg Dez 13, 2010 01:23
por Lorettto » Seg Dez 13, 2010 01:23
Isso resolve de modo direto a qualquer questão de maior , menor de potências gigantes !! Claro, apenas quando estamos elevados a potências iguais, aí a base determina mesmo.
Editado pela última vez por
Lorettto em Seg Dez 13, 2010 01:27, em um total de 1 vez.
-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Maior valor
por thadeu » Qua Nov 25, 2009 16:17
- 4 Respostas
- 2960 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:14
Álgebra Elementar
-
- maior fator primo
por Marcos Ivan » Sáb Ago 21, 2010 12:29
- 1 Respostas
- 2410 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 17:28
Geometria Analítica
-
- Maior valor da inequação
por maria cleide » Dom Mai 29, 2011 17:35
- 8 Respostas
- 4611 Exibições
- Última mensagem por maria cleide

Dom Jun 05, 2011 18:25
Sistemas de Equações
-
- derivada de ordem maior!
por giulioaltoe » Sex Jul 29, 2011 16:27
- 2 Respostas
- 1823 Exibições
- Última mensagem por giulioaltoe

Sex Jul 29, 2011 16:42
Cálculo: Limites, Derivadas e Integrais
-
- Demonstração de a²+b²+ab é maior ou igual a 0
por JessicaHayanne » Qui Mar 21, 2013 17:41
- 1 Respostas
- 3212 Exibições
- Última mensagem por e8group

Qui Mar 21, 2013 19:17
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
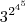 ou
ou 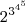 ?
?

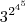 ou
ou 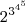 ?
?

 . Suponha que
. Suponha que 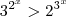 .
.
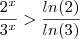
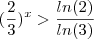
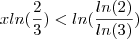
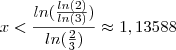
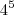 , então
, então 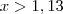 (absurdo)
(absurdo)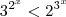 .
.






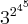
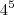 = 1024
= 1024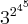 =
=  =
= 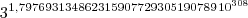

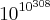
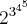
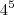 = 1024
= 1024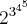 =
= 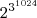 =
= 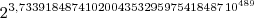


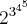 é maior que
é maior que 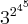

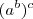 mas como tem aquela indicação que não pode fazer isso, então a conclusão q eu tinha chegado tb q era:
mas como tem aquela indicação que não pode fazer isso, então a conclusão q eu tinha chegado tb q era:  é falsa por potenciação feita errado.
é falsa por potenciação feita errado.




 ou
ou  ?
?


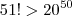 .
.