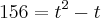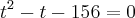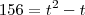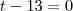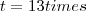A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por anapaulausp » Ter Dez 08, 2009 17:45
por anapaulausp » Ter Dez 08, 2009 17:45
Estou estudanto para concursos publicos e fazendo alguns simulados, tive dificuldade em resolver esse probleminha, podem me ajudar???
Ao organizar a tabela de jogos de futebol de seu bairro, Maurício observou que havia uma relação entre o número
de times participantes e o número de partidas que deveriam ser disputadas. Essa relação foi escrita sob a forma de uma
função: F(t) = t2 – t, onde t é o número de times participantes e F(t) representa o total de partidas em função de t.
Em 2007, o total de partidas disputadas em um só campeonato chegou a 156. Ou seja, em 2007 estavam envolvidos no
campeonato um total de.....
-
anapaulausp
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Nov 17, 2009 16:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Ter Dez 08, 2009 18:27
por Cleyson007 » Ter Dez 08, 2009 18:27
Boa tarde Ana Paula!
O exercício obedece a seguinte função:
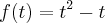
. Como foram disputadas 156 partidas,

...
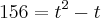
Feito isso, basta achar o valor de t (números de envolvidos no campeonato).
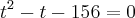
Ana Paula, aqui temos uma equação do segundo grau. Basta resolvê-la encontrando os valores de t

Fique atenta quanto aos valores encontrados para t (o valor negativo não satisfaz), ok?
Comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por anapaulausp » Qua Dez 09, 2009 09:37
por anapaulausp » Qua Dez 09, 2009 09:37
Valeu!!!
Mais uma vez
OBRIGADA
-
anapaulausp
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Nov 17, 2009 16:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por leandro moraes » Ter Jan 12, 2010 23:47
por leandro moraes » Ter Jan 12, 2010 23:47
gostaria de saber como fasso para postar uma pergunta? sou novato no forum.
-
leandro moraes
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Ter Jan 12, 2010 23:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: contabilidade
- Andamento: formado
 por DanielFerreira » Seg Mar 15, 2010 13:17
por DanielFerreira » Seg Mar 15, 2010 13:17
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por -daniel15asv » Qui Ago 02, 2012 20:16
por -daniel15asv » Qui Ago 02, 2012 20:16
ta errado o gabarito é 7
-
-daniel15asv
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Ago 02, 2012 19:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


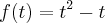 . Como foram disputadas 156 partidas,
. Como foram disputadas 156 partidas,  ...
...