A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por geriane » Qui Abr 22, 2010 16:01
por geriane » Qui Abr 22, 2010 16:01
Em um grupo de três crianças de idades diferentes foi notado que a soma das duas idades menores menos a maior é igual a 2 anos e que a menor idade mais o dobro da maior é igual a 28 anos. As idades são números inteiros positivos. Dentre todas as possibilidades, existe uma em que a soma das idades das crianças é a maior possível, observando-se sempre o fato de as crianças terem idades diferentes. Essa soma, em anos, é? a resposta é 26 mas o meu sempre dá 22.
-
geriane
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Sáb Abr 03, 2010 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura
- Andamento: formado
 por Molina » Qui Abr 22, 2010 20:48
por Molina » Qui Abr 22, 2010 20:48
Boa noite, geriane.
Primeiramente chamei
a,
b e
c as idades das crianças, respectivamente, da mais nova para a mais velha. O problema nos traz duas informações que poderemos montar duas equações que nos ajudaram a encontrar esse valor. São elas:
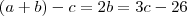
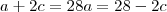
Note o seguinte, como as 3 idades são positivas, e utilizando a segunda equação, o valor de
c não será 14, pois
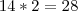
e a idade de a teria que ser 0 (o que não é positiva).
c também não será 13, pois
a e
b teriam a mesma idade (4 anos). Já

, teríamos
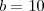
e
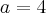
o que satisfaz as condiçoes do problema e a soma é 26. Tomando
c como qualquer outro valor não dá certo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- me ajudem ai !!
por weverton » Ter Jun 15, 2010 23:45
- 1 Respostas
- 1640 Exibições
- Última mensagem por Mathmatematica

Qua Jun 16, 2010 01:18
Sistemas de Equações
-
- me ajudem ai!!!
 por weverton » Qui Jul 08, 2010 17:15
por weverton » Qui Jul 08, 2010 17:15
- 2 Respostas
- 8409 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 08, 2010 19:50
Estatística
-
- me ajudem
por weverton » Qui Out 07, 2010 17:34
- 1 Respostas
- 1664 Exibições
- Última mensagem por MarceloFantini

Qui Out 07, 2010 18:07
Geometria Analítica
-
- me ajudem
por weverton » Seg Nov 08, 2010 16:11
- 7 Respostas
- 3948 Exibições
- Última mensagem por MarceloFantini

Qua Nov 10, 2010 01:43
Logaritmos
-
- Me ajudem!
por paulag » Qua Nov 10, 2010 21:30
- 1 Respostas
- 1440 Exibições
- Última mensagem por paulag

Qua Nov 10, 2010 23:12
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



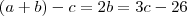
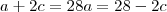
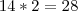 e a idade de a teria que ser 0 (o que não é positiva). c também não será 13, pois a e b teriam a mesma idade (4 anos). Já
e a idade de a teria que ser 0 (o que não é positiva). c também não será 13, pois a e b teriam a mesma idade (4 anos). Já  , teríamos
, teríamos 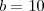 e
e 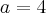 o que satisfaz as condiçoes do problema e a soma é 26. Tomando c como qualquer outro valor não dá certo.
o que satisfaz as condiçoes do problema e a soma é 26. Tomando c como qualquer outro valor não dá certo.
