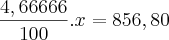A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Liliani » Qua Abr 07, 2010 17:05
por Liliani » Qua Abr 07, 2010 17:05
Calcule o capital que se deve aplicar a taxa de 8% ao ano durante 7 meses para obter juro de R$856,80.
Fiz o seguinte: J=CIT/100
856,80=C.0,66 (QUE É 8:12).7/100 == 856,80=0,0462C == C= 18528,13
MAS A RESPOSTA NO LIVRO É: 18360,00
POR FAVOR, ONDE ERRO?
-
Liliani
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Fev 23, 2010 14:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por estudandoMat » Qua Abr 07, 2010 17:37
por estudandoMat » Qua Abr 07, 2010 17:37
Primeiro vc verifica qts % são em 7 meses:
8% = 12 meses ( Regra de 3 )
x = 7 meses
x = 4,6666666...
Agora, descobrir de qual valor 4,66666% corresponde a 856,80
0,046666.x = 856,80 ou
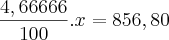
x = 18360,00
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- trigonometria simples mas o resultado não bate certo.
 por tiagofe » Sex Mai 06, 2011 17:31
por tiagofe » Sex Mai 06, 2011 17:31
- 4 Respostas
- 5230 Exibições
- Última mensagem por claudinho

Dom Jun 12, 2011 12:20
Trigonometria
-
- [Função Composta] Resultado não bate com o do gabarito
por Richard Oliveira » Sáb Nov 12, 2011 14:59
- 3 Respostas
- 4234 Exibições
- Última mensagem por Richard Oliveira

Seg Nov 14, 2011 00:50
Funções
-
- Eu já tentei de diversas maneiras mas o resultado dá sempre
por sergiomorales » Qui Jun 02, 2011 12:28
- 1 Respostas
- 2185 Exibições
- Última mensagem por carlosalesouza

Sáb Jun 04, 2011 02:34
Binômio de Newton
-
- Eu tentei, tentei e não consegui...
por phelipe » Seg Fev 08, 2010 12:40
- 4 Respostas
- 4891 Exibições
- Última mensagem por Elcioschin

Ter Fev 09, 2010 08:26
Desafios Médios
-
- Tentei, tentei e nada
por Thiago1986Iz » Sex Jul 22, 2016 18:02
- 2 Respostas
- 3249 Exibições
- Última mensagem por Thiago1986Iz

Sáb Jul 23, 2016 20:56
Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.