Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por viduani » Seg Ago 13, 2012 19:15
por viduani » Seg Ago 13, 2012 19:15
Bom dia a todos os amigos e em especial àquele que tentará me ajudar neste problema. Mesmo se tratando de um problema do 2º grau e que foi feito através de sistema, não foi possível compreender a sua resolução. O problema foi descrito assim: No texto do livro teórico, LI TA-CHAO, organizou em 1918 a sociedade de pesquisas marxistas, um pequeno círculo de estudos com a finalidade de estudar e analisar a experiência russa. Acolheu, nesse grupo, um jovem humanista que também trabalhava na biblioteca como ajudante: MAO TSÉ-tung. De início, ele propôs distribuir para o grupo de estudos 360 livros. No dia da distribuição, faltaram 3 participantes e, desse modo, cada um dos que estavam presentes recebeu 10 livros a mais. Quantos participantes tinha esse grupo?
A proposta do professor foi a seguinte:
P.L=360 ---------------------L=360/P
(L + 10)(P - 3)= 360
Não entendi como ele armou esse esquema e porque ao fazer o sistema pelo método da substituição ele usou a equação transformada na equação debaixo sem ao menos tentar desenvolvê-la. Um forte abraço aos amigos.
-
viduani
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Jul 13, 2012 20:03
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: curso m3
- Andamento: cursando
 por DanielFerreira » Seg Ago 13, 2012 19:47
por DanielFerreira » Seg Ago 13, 2012 19:47
Viduani,
boa noite!
Quanto ao 'esquema':
número de participantes:

número de livros:
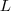
Ao multiplicar a quantidade total de
participantes com a quantidade de
livros de cada um deles, tem-se o número total de livro, daí:

;
Três participantes faltaram, então

;
Cada um deles recebeu 10 livros a mais,

, com isso,

Quanto a última dúvida, seu professou apenas optou pela maneira que julgou mais simples. Ele poderia ter desenvolvido...
Comente qualquer dúvida!
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problemas de 1 grau
por henriquefreitas » Dom Abr 24, 2011 06:27
- 1 Respostas
- 2037 Exibições
- Última mensagem por SidneySantos

Dom Abr 24, 2011 08:03
Álgebra Elementar
-
- Problemas de 1 grau
por henriquefreitas » Dom Abr 24, 2011 17:30
- 6 Respostas
- 3501 Exibições
- Última mensagem por LuizAquino

Dom Abr 24, 2011 21:25
Álgebra Elementar
-
- [porcentagem] problemas de 1° grau
por heroncius » Qua Set 05, 2007 01:02
- 2 Respostas
- 4474 Exibições
- Última mensagem por heroncius

Qua Set 05, 2007 14:10
Álgebra Elementar
-
- problemas com equacoes de 1 grau
por luanxd » Qua Jan 27, 2010 23:14
- 2 Respostas
- 2345 Exibições
- Última mensagem por luanxd

Sáb Jan 30, 2010 23:31
Polinômios
-
- Problemas do segundo grau II
por Alessandra Cezario » Seg Mai 02, 2011 17:56
- 1 Respostas
- 2608 Exibições
- Última mensagem por TheoFerraz

Seg Mai 02, 2011 18:31
Problemas do Cotidiano
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



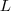
 ;
; ;
; , com isso,
, com isso, 


 .
.



