Bom dia, preciso de uma ajuda para entender essas questões de concursos.
Uma cabine de uma rodovia arrecadou 3.360 reais com a cobrança de pedágio de 800 veículos, entre motos, carros de passeio e caminhões, que passaram por lá durante 1 hora. Sabe-se que nessa cabine e nesse horário, considerando-se os veículos que pagaram pedágio, o número de carros de passeio foi o triplo da quantidade de motos e que os preços cobrados foram os da lista abaixo. Portanto, pode-se afirmar que a quantidade de caminhões que passaram por essa cabine, pagando pedágio, foi de:
Moto - R$ 1,80
Carro de passeio - R$ 4,20
Caminhão - R$ 6,00
Desde já agradeço.


 , carros de passeio de
, carros de passeio de  e caminhões de
e caminhões de  , temos:
, temos: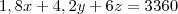
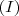

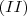

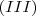
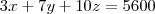
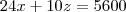
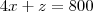
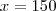
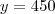
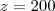


 , certo? Eu apenas substitui nas equações
, certo? Eu apenas substitui nas equações 
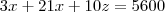
 ;
;
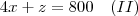 ;
;

