MInha intenção não foi parecer estar de má vontade. É recorrente alunos buscando resoluções completas para trabalhos e afins. Mas, ok. Você me pareceu interessada.
Uma função do tipo
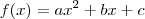
possui um ponto de extremo em
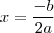
. Isto é, aplicando
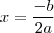
em

você calcula-rá o seu maior ou menor valor. Se
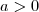
então o ponto é de mínimo e se
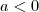
o ponto é de máximo. Naturalmente, calculando
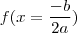
você chegará em
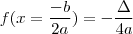
(onde este delta é o mesmo da fórmula de resolução de equações de 2º grau) que é o maior ou menor valor atingido pela função.
Como a sua função é
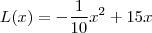
o ponto extremo será de máximo, pois
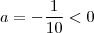
. Ele ocorre em
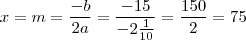
com valor
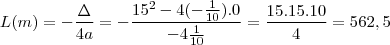
Agora, o exercicio manda fazer
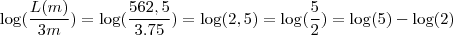
.
Basta aplicar as propriedade do logaritmo do quociente para chegar na resposta q eu escrevi. Porém, esse valor não está presente na questão. Ou eu calculei algum numero errado ou deve haver outro engano.



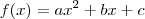 possui um ponto de extremo em
possui um ponto de extremo em 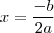 . Isto é, aplicando
. Isto é, aplicando  você calcula-rá o seu maior ou menor valor. Se
você calcula-rá o seu maior ou menor valor. Se 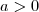 então o ponto é de mínimo e se
então o ponto é de mínimo e se 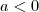 o ponto é de máximo. Naturalmente, calculando
o ponto é de máximo. Naturalmente, calculando 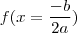 você chegará em
você chegará em 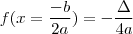 (onde este delta é o mesmo da fórmula de resolução de equações de 2º grau) que é o maior ou menor valor atingido pela função.
(onde este delta é o mesmo da fórmula de resolução de equações de 2º grau) que é o maior ou menor valor atingido pela função.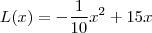 o ponto extremo será de máximo, pois
o ponto extremo será de máximo, pois 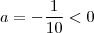 . Ele ocorre em
. Ele ocorre em 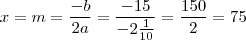
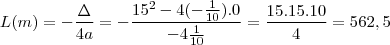
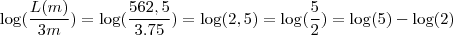 .
.