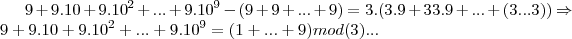-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480342 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 540498 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 504375 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 730141 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2167958 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Wermeson Silva » Qui Jul 27, 2017 16:30
por Wermeson Silva » Qui Jul 27, 2017 16:30
A questão é: "qual a fórmula gera o menor múltiplo, formado apenas por algarismos 9, de um número impar?"
-
Wermeson Silva
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Jul 27, 2017 16:09
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em eletrotécnica
- Andamento: cursando
 por adauto martins » Qui Set 07, 2017 16:58
por adauto martins » Qui Set 07, 2017 16:58
os divisores de 9,sao{1,3,9}...
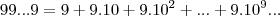
,como 9 é multiplo de 3,teremos:
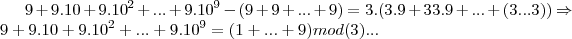
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.A. e não múltiplos
por Cleyson007 » Qui Dez 24, 2009 11:45
- 2 Respostas
- 3192 Exibições
- Última mensagem por Cleyson007

Qui Dez 24, 2009 16:36
Progressões
-
- multiplos
por jose henrique » Sáb Ago 21, 2010 22:25
- 1 Respostas
- 2083 Exibições
- Última mensagem por DanielRJ

Sáb Ago 21, 2010 23:21
Álgebra Elementar
-
- multiplos
por jose henrique » Sáb Ago 21, 2010 22:28
- 2 Respostas
- 2471 Exibições
- Última mensagem por jose henrique

Sáb Ago 21, 2010 23:27
Álgebra Elementar
-
- Multiplos
por loran » Qua Dez 15, 2010 18:02
- 1 Respostas
- 2156 Exibições
- Última mensagem por MarceloFantini

Qui Dez 16, 2010 00:15
Álgebra Elementar
-
- multiplos de 7
por Gladimir » Sáb Fev 01, 2014 00:15
- 1 Respostas
- 2084 Exibições
- Última mensagem por Russman

Sáb Fev 01, 2014 00:55
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



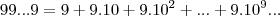 ,como 9 é multiplo de 3,teremos:
,como 9 é multiplo de 3,teremos: