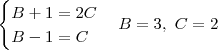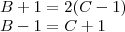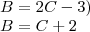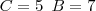Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
por admin » Sáb Jul 21, 2007 01:12
Um cavalo e um burro caminhavam juntos, carregando cada um pesados sacos. Como o cavalo reclamava muito de sua pesada carga, disse-lhe o burro: De que te queixas? Se me desses um saco, minha carga seria o dobro da tua, mas se eu te der um saco, tua carga será igual a minha. Quantos sacos cada um deles levava?
-
admin
- Colaborador Administrador - Professor
-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
por Marcampucio » Sáb Mar 14, 2009 18:56
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário
-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
por [++] » Qui Jul 16, 2009 00:51
Marcampucio escreveu: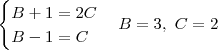
vc está dizendo q o burro leva 3 sacos e o cavalo leva 2, mas se o burro der um saco ao cavalo 3-2 o burro fica com 2 sacos e o cavalo com 3 , então não está certo, o certo (q eu acho) é o burro com 7 e o cavalo com 5: se o burro der um saco para o cavalo os dois ficam o 6, mas se o cavalo der um para o burro, o burro fica com 8 o cavalo com 4, sendo 8 o dobro de 4!!!
ok? se estiver errado, ou tiver outras soluçôes me avisem
-
[++]
- Novo Usuário
-
- Mensagens: 9
- Registrado em: Qua Jul 15, 2009 23:55
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
por Marcampucio » Qui Jul 16, 2009 01:13
Oops! errei na montagem da equação, os sacos vão de um para o outro.
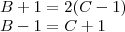
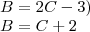
agora sim
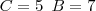
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário
-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.
Em
substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.
2)Na equação
não existem zeros.Senão vejamos
Completando o quadrado,
As coordenadas do vertice da parabola são
O eixo de simetria é a reta
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
