“7. Uma v.a X tem distribuição normal, com média 100 e desvio padrão 10.
(a) Qual a P (90 < X < 100)?
(b) Se
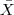 for a média de uma amostra de 16 elementos retirados dessa população, calcule P (90 < X < 100).
for a média de uma amostra de 16 elementos retirados dessa população, calcule P (90 < X < 100).(c) (...)”
a) P(90 < X < 110) = P( x < 110) - p (x < 90) = 0,84134 - 0,15866 = 0,68268
b) ???



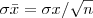 ;
; 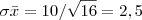
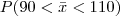 para N~(100,2,5)
para N~(100,2,5)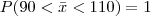
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)