Olá, vou ter exame e alguns exercicios em que preciso de achar a probabilidade eu tenho muitas dúvidas.
O exercicios é :
Para fabricar um determinado produto uma empresa utiliza 3 maquinas, M1, M2 e
M3. Sabe-se que: i) a maquina M1 fabrica 40% da produc~ao total da empresa; ii)
a percentagem de produtos defeituosos fabricados pelas maquinas M1, M2 e M3 e,
respectivamente, 3%, 5% e 8%; iii) 5% da produc~ao total e defeituosa.
(a) Calcule a percentagem da produc~ao total fabricada pela maquina M3.
(b) Sabendo que um produto escolhido ao acaso n~ao e defeituoso, qual a probabilidade
de ter sido fabricado pela maquina M2?
Eu do que recolhi os dados percebi que a máquina M1 tem 40% da produção total, depois tem 3% de produtos fabricados, ni ponto iii) diz que a produção total de produtos defeituosos é 5 % e daí eu não consigo perceber qual a informação útil para achar a produçaõ total de M2 e M3.
E o produto não ser defeituoso é 1 - 0.05 = 0.95 ?
Estes exercicios para mim são muito confusos, se alguém me puder ajudar, agradeço.
Cumprimentos,
Ana


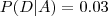

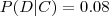
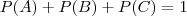
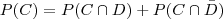
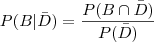




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.