 por Yargo » Dom Jul 15, 2018 22:23
por Yargo » Dom Jul 15, 2018 22:23
Uma variável aleatória X possui uma distribuição de probabilidades representada pela distribuição Normal padrão. Sabendo-se que

, pergunta-se:
(a) Qual é a distribuição de probabilidades de Y?
(b) Qual é o valor extremo mais provável de Y no caso de N=1000 ocorrências desta variável?
OBSERVAÇÕES:
(1)
Pelo que sei, para N(0,1):
PDF vale
![\phi(x)=\frac{{e}^{\frac{{-x}^{2}}{2}}}{\sqrt[]{2\pi}} \phi(x)=\frac{{e}^{\frac{{-x}^{2}}{2}}}{\sqrt[]{2\pi}}](/latexrender/pictures/0997ee1944bc6e57083804be52d4dcb1.png)
e CDF vale
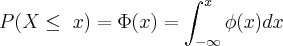
(2)
Este é o primeiro de uma lista de 6 problemas. Ofereço 100 reais para a solução da lista (e-mail para: yargop@hotmail.com).
Muito grato pela atenção.
-
Yargo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jul 15, 2018 21:37
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidades - cálculo probabilidades e condicionada
por carlosmartins » Dom Set 21, 2014 18:58
- 0 Respostas
- 2954 Exibições
- Última mensagem por carlosmartins

Dom Set 21, 2014 18:58
Probabilidade
-
- probabilidades
 por edwilsoncrep » Qui Mar 04, 2010 19:28
por edwilsoncrep » Qui Mar 04, 2010 19:28
- 3 Respostas
- 3282 Exibições
- Última mensagem por edwilsoncrep

Qui Mar 04, 2010 19:49
Estatística
-
- Probabilidades!
por pferraz » Qui Out 27, 2011 22:53
- 3 Respostas
- 7067 Exibições
- Última mensagem por Russman

Qua Dez 23, 2015 22:04
Estatística
-
- Probabilidades
por matematicaead » Qua Nov 16, 2011 13:53
- 1 Respostas
- 2227 Exibições
- Última mensagem por Neperiano

Qua Nov 23, 2011 16:32
Estatística
-
- probabilidades
por cris_leite » Seg Jan 23, 2012 21:17
- 9 Respostas
- 5551 Exibições
- Última mensagem por fraol

Dom Jan 29, 2012 12:41
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , pergunta-se:
, pergunta-se:![\phi(x)=\frac{{e}^{\frac{{-x}^{2}}{2}}}{\sqrt[]{2\pi}} \phi(x)=\frac{{e}^{\frac{{-x}^{2}}{2}}}{\sqrt[]{2\pi}}](/latexrender/pictures/0997ee1944bc6e57083804be52d4dcb1.png)
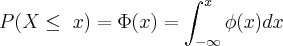




 , avisa que eu resolvo.
, avisa que eu resolvo.

