Preciso de ajuda nesta questão.
Numa lanchonete são vendidos sucos de fruta servidos em copos grandes e pequenos sendo que o preço do copo
pequeno custa dois terços do preço do copo grande. Se o valor pago por uma pessoa que comprar um copo de cada
tamanho é igual a R$ 8,00, então a diferença de preço entre os dois tamanhos de suco é igual a: Resposta (1,6)



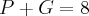
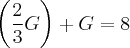
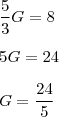 -> Este é o preço do copo grande. Pra descobrir o preço do pequeno, basta substituir na primeira relação encontrada:
-> Este é o preço do copo grande. Pra descobrir o preço do pequeno, basta substituir na primeira relação encontrada:


 .
.
 :
: