Escolhendo-se, ao acaso, uma comissão de 4 pessoas, a probabilidade de o Dr. House ou a Dra.Cuddy pertecerem a essa comissão é de
01)
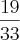
02)

03)

04)
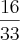
05)
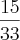
Estou resolvendo da seguinte forma:

onde :
n(A) é 2x1x10x9= 180
n(S) é C12,4= 495
simplifico tudo po 15 e acho
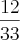
alguem pode me ajudar!



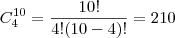
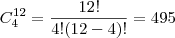
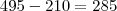
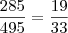


 .
.
 :
: