-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477812 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529144 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 492699 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 698056 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2107796 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por alezeit » Qui Jan 02, 2014 12:53
por alezeit » Qui Jan 02, 2014 12:53
Olá , td bem?
Gostaria de sdaber qual a probabilidade de acertar 3 dezenas na mega sena jogasndo o jogo de R$ 2,00 que consiste em 6 dezenas;A probabilidade só é mostrada até 4 acertos e também gostaria de saber como é feito essse cálculo.
Obrigado
Alexandre
-
alezeit
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Jan 02, 2014 12:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administracao
- Andamento: formado
 por Baltuilhe » Dom Jan 21, 2018 03:55
por Baltuilhe » Dom Jan 21, 2018 03:55
Boa noite!
Basta calcular o seguinte:
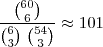
Para calcular use o seguinte:
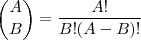
Ou seja, acertar 3 números é 1 chance em 101.
Vou deixar a fórmula 'genérica' aqui pra vc:
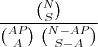
, onde:
N = quantidade de números da cartela
S = quantidade de números sorteados
AP = quantidade de números apostados
A = quantidade de números (acerto)
Só

Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Reportagem sobre Mega Sena - 31/08/07
por admin » Dom Set 02, 2007 04:52
- 5 Respostas
- 15802 Exibições
- Última mensagem por admin

Seg Dez 03, 2007 15:50
Problemas do Cotidiano
-
- Números em sequencia na Mega Sena
por fduarte » Qua Set 02, 2009 01:48
- 4 Respostas
- 8128 Exibições
- Última mensagem por vancouver

Qui Mar 10, 2011 19:43
Estatística
-
- Cálculo da probabilidade de acerto na Mega Sena
por admin » Seg Dez 03, 2007 15:54
- 1 Respostas
- 11592 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 19:43
Problemas do Cotidiano
-
- Calcular a quantidade de prêmios da mega sena
por julinternauta » Ter Mai 17, 2011 13:58
- 1 Respostas
- 6966 Exibições
- Última mensagem por julinternauta

Qui Mai 26, 2011 13:57
Estatística
-
- mediana...não consigo acertar
por TEKA » Seg Mar 29, 2010 11:38
- 1 Respostas
- 3022 Exibições
- Última mensagem por Neperiano

Sex Set 17, 2010 15:36
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


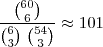
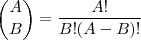
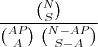 , onde:
, onde: Espero ter ajudado!
Espero ter ajudado!