a)provar que U tem uma função densidade contínua f(u) dado por:
f(u)= u se 0<u<1,
2-u se 1<u<2
0 para os restantes valores de u.
b) Definir, de modo análogo uma densidade contínua f(v) para V.
c) Verificar se U e V são ou não independentes.
Bem na letra a eu fiz quase tudo, mas não consigo saber como lhufas ele separou os valor de f(u), para mim deveria ser só um valor entre (0,2).
Fica assim:
f(y)=f(x)=1, para x,y em [0,1]; essas são as densidades probabilisticas de Y e X
O jacobiano fica 1/2
e como ele disse que as funções são independentes f(x,y)=f(x)*f(y). Daí um integrei tudo e cheguei a:
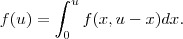daí achei que f(x) é igual a u para u em [0,2]
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.