 por Bravim » Qui Out 03, 2013 04:56
por Bravim » Qui Out 03, 2013 04:56
Uma variável aleatória X tem uma função de repartição(mesma coisa que distribuição acumulada)contínua F e uma função densidade f. A função densidade tem as propriedades:
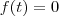
se
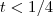
,
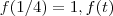
é linear se
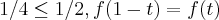
para todo t.
a)trace o gráfico de f(Como será difícil colocar o gráfico, a fórmula de f já basta).
b)Dar um conjunto de fórmulas que definam F e traçar o seu gráfico.
c)Calcular as probabilidades seguintes :
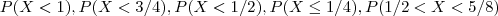
Bem, o que eu encontrei foi:
f(t)=0, se t<1/4
f(t)=0, se t>3/4
f(3/4)=1.
Ah sim, muito provavelmte a figura será simétrica pelo eixo x=1/2
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função de variael aleatoria
por Mppl » Qui Jan 27, 2011 08:11
- 0 Respostas
- 1153 Exibições
- Última mensagem por Mppl

Qui Jan 27, 2011 08:11
Estatística
-
- Variável Aleatória Exercícios
por snoffao » Ter Nov 25, 2014 16:42
- 0 Respostas
- 2392 Exibições
- Última mensagem por snoffao

Ter Nov 25, 2014 16:42
Probabilidade
-
- Variável Aleatória Exercício 2
por snoffao » Ter Nov 25, 2014 16:46
- 0 Respostas
- 3591 Exibições
- Última mensagem por snoffao

Ter Nov 25, 2014 16:46
Probabilidade
-
- [Probabilidade]Função de variável aleatória bidimensional.
por Bravim » Dom Out 06, 2013 16:57
- 0 Respostas
- 1297 Exibições
- Última mensagem por Bravim

Dom Out 06, 2013 16:57
Probabilidade
-
- Média e variância de uma amostra aleatoria simples c/repsção
por Razoli » Qui Set 17, 2015 10:35
- 0 Respostas
- 1764 Exibições
- Última mensagem por Razoli

Qui Set 17, 2015 10:35
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
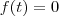 se
se 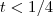 ,
,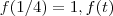 é linear se
é linear se 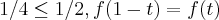 para todo t.
para todo t.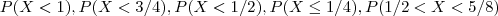




 .
.



