"Quatro pássaros pousam em uma rede de distribuição elétrica que tem quatro fios paralelos. A probabilidade de que em cada fio pouse apenas um
pássaro é ?"
a) 3/32
b) 1/256
c) 1/24
d) 1/4
e) 3/4
Eu tentei resolver da seguinte forma:
1° passo: Construo uma matriz para identificar as possibilidades de organização dos pássaros no espaço.
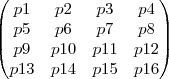
Em que (p1,p2,p3,p4) por exemplo significaria os pássaros estarem um em cada fio
e (p1,p5,p9,p13) por exemplo significaria os pássaros estarem no mesmo fio.
2° passo: Usando o raciocinio anterior descubro o valor de n(
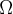 ) que seria:
) que seria: 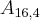 =
= 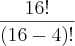 = 43680
= 436803° passo: Agora eu tenho que descobrir quantas possibilidades diferentes eu tenho para que cada pássaro esteja num fio diferente.
 ________________
____________________
 ___________
___________________
 _______
_____________________

Seria 4 passaros contados de 4 em 4 =
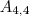 = 24
= 24Então n(E) = 24
4° passo: Agora é ja definidos n(E) e n(
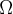 ) é só fazer:
) é só fazer: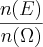 =
= 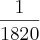
Só que não é esse o resultado da questão...
Obs1. Eu usei arranjo ao invés de combinação porque os pássaros são entidades diferentes entre si, tal como as posições dos pássaros.
Obs2. Eu usei muito LaTeX porque to testando e aprendendo
Obs3. Eu só tenho o ensino médio ( ainda por cima em ensino publico), então cuidado com as respostas XD.
Eu queria saber onde eu errei, se alguém puder me responder ficarei muito grato
Valeu.



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)