 por benni » Dom Mai 08, 2011 12:03
por benni » Dom Mai 08, 2011 12:03
Assuma que X é uma variavel aleatória e que A e B são eventos em R .As seguintes afirmações trabalham com o conjunto imagem inversa e sua preservação por oprerações em conjuntos.PROVE O RESULTADO.
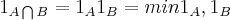
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por benni » Qua Mai 11, 2011 16:14
por benni » Qua Mai 11, 2011 16:14
Sempre eu.rasras...
Pela probabilidade da intersecção de eventos, temos: P( A/B) =P(A)
Donde : usando a probabilidade condicional, temos:P(A) = P(A inter B)/ P(B)
Portanto, dois eventos A e B estão ditos independentes se
P(A inter B) =P(A).P(B)
Pela sua inversa e considerando como uma função , temos que: 1/P(A interB) =1/P(A) .1/P(B)
O que está sendo citado aqui é que o inverso da intersecção de A e B é igual ao inverso do evento A vezes o inverso do evento B. Como função
Então prova-se o que se pediu.
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por psdias » Ter Mai 22, 2012 09:42
por psdias » Ter Mai 22, 2012 09:42
Olá !
No material de apoio do site da REDEFOR há dois arquivos PDF que irão ajudar a responder essa questão.
Obs.: O símbolo 1AUB (com o AUB estando como subscrito, ou seja, subíndice) significa "Função característica".
Definição de função característica:
http://www.mediafire.com/view/?yoahuq19676dp91Exercícios resolvidos:
http://www.mediafire.com/view/?q18tgjqm0wu8j7d
-
psdias
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Nov 22, 2011 18:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: LICENCIATURA EM MATEMÁTICA
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probablidade] variáveis aleatórias
por 1paulo » Sáb Mai 17, 2014 13:06
- 0 Respostas
- 2230 Exibições
- Última mensagem por 1paulo

Sáb Mai 17, 2014 13:06
Probabilidade
-
- varíaveis aleatórias contínuas conjuntas
por gprestes » Qua Nov 24, 2010 08:38
- 0 Respostas
- 2542 Exibições
- Última mensagem por gprestes

Qua Nov 24, 2010 08:38
Estatística
-
- Prova com Variáveis Aleatórias Independentes
 por EREGON » Seg Mai 18, 2015 09:02
por EREGON » Seg Mai 18, 2015 09:02
- 0 Respostas
- 1279 Exibições
- Última mensagem por EREGON

Seg Mai 18, 2015 09:02
Probabilidade
-
- [Variáveis Aleatórias] Esperança Matemática
 por guisore_09 » Ter Dez 29, 2015 08:58
por guisore_09 » Ter Dez 29, 2015 08:58
- 4 Respostas
- 11090 Exibições
- Última mensagem por guisore_09

Dom Jan 03, 2016 10:20
Estatística
-
- Probabilidades de variáveis aleatórias discretas e continuas
por pogalski » Dom Jun 05, 2011 11:03
- 2 Respostas
- 3037 Exibições
- Última mensagem por MarceloFantini

Qua Jun 22, 2011 00:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
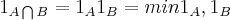


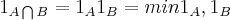



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.