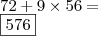Darlan2009,
boa noite!
A saber, os múltiplos de 10 compreendidos entre 100 e 9999 são: {110, 120, 130,..., 9980, 9990}.
MAS, os algarismos são distintos, então:
Com três algarismos:
{120, 130, 140, 150, 160, 170, 180, 190}
{210, 230, 240, 250, 260, 270, 280, 290}
...
{910, 920, 930, 940, 950, 960, 970, 980}
8 X 9 =
72Com quatro algarismos:
{1230, 1240, 1250, 1260, 1270, 1280, 1290}
{1320, 1340, 1350, 1360, 1370, 1380, 1390}
...
{1920, 1930, 1940, 1950, 1960, 1970, 1980}
7 X 8 =
56 Note que, há 56 múltiplos de dez quando a unidade de milhar é UM. Quando a unidade de milhar começar com DOIS, teremos mais 56 múltiplos, e assim...
Portanto,
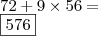
Tem o gabarito?