(ITA-1957)sao dados os objetos A,B,C,D.responder as perguntas seguintes(se tiverem sentido):
a)quantos sao os arranjos desses objetos,tomados 3 a 3?
b)quantas as combinaçoes,tomados 2 a 2?
c)quantas as permutaçoes,tomados 3 a 3?
escrever os arranjos desses objetos,tomados 2 a 2;escrever as combinaçoes 2 a 2;escrever as permutaços dos 4 objetos.
em que se disteguem as combinaçoes dos arranjos?


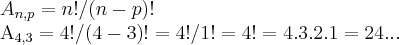
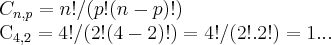

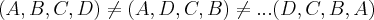
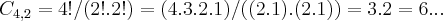
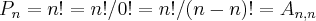


 , avisa que eu resolvo.
, avisa que eu resolvo.

