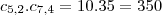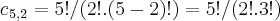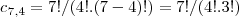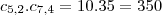soluçao:
aqui usaremos o principio fundamental da contagem e tbem a formula
das combinaçoes.temos uma 6-upla,que no caso,nao pede nada de ordem,
uma restriçao de postagem,uma sequencia ou similar, das bolas brancas;somente q. 2 bolas brancas
sempre estarao presentes.portanto uma combinaçao.
seja a 6-upla (-,-,-,-,-,-)...
1)entre as 5 bolas brancas precisaremos de 2,entao teremos:
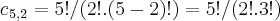
2)das 12 bolas,como retirei 5 bolas(brancas)restarao 7 bolas(pretas)
e na 6-upla,4 posiçoes a serem preenchidas por estas bolas,logo:
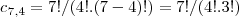
entao como,pela condiçao colocada no problema de sempre termos duas bolas brancas,usaremos o princ.fund. contagem...
teremos: