soluçao:
dos 10 dez algarismos 3,3,3,4,4,5,6,7,7,7,ficaremos
com 3,3,6,7,7,pois o numero fixo 34475 tera que estar no final,e
retiramos os numeros 1 num.3,2 num.4,1 num.5 e 1 num.7 da sequencia dada(33...6..7)
entao os possiveis numeros a serem construidos,na 10-upla(-,-,-,-,-,3,4,4,7,5) serao:
da 10-upla(-,-,-,-,-,3,4,4,7,5), com 2!(num.3), 2!(num.7) e 1!(num.6)repetiçoes ;trabalharemos com
a 5-upla(3,3,6,7,7),no qual obteremos:
(5 possib.,4 possib.,3 possib.,2 possib.,1 possib.) que implica,pelo princ.multiplicativo em:
5.4.3.2.1=5!,dividindo pelas repetiçoes(2!(num.3),1!(num.6),2!(num.7),termos:
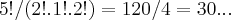



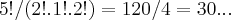


 .
.
 :
: