encontrei no livro "fundamentos de matematica elementar-vol.5-samuel hazzan-ed.1981,pag.43-e",uma soluçao para tal problema e situaçao...desculpe-me a lana pela minha colocaçao de nao haver soluçao,devido a ma formulaçao.
vamos a colocaçao,soluçao dada pelo autor:
esse problema pode ser formulado da seguinte maneira:
"quantas soluçao inteiras e nao negativas existem para
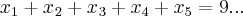
,que é uma equaçao diofantina,com a ressalva de
achar raizes inteiras e positivas...a forma didatica dada pelo autor é:
barras para separar as formas possiveis de soluçao e pontos para as devidas raizes,por exemplo:
possiveis soluçoes seriam (..I...I.I..I.),(.I..I...I..I.),...ou seja seriam necessarias 4 barras para separar os 9 pontos"soluçoes",
a qual deria como total de soluçoes a combinaçao
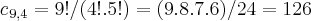



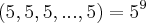
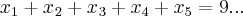 ,que é uma equaçao diofantina,com a ressalva de
,que é uma equaçao diofantina,com a ressalva de 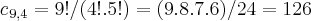
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.