-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480135 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 538865 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 502723 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 725528 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2160846 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por pribl17- » Sex Ago 18, 2017 17:57
por pribl17- » Sex Ago 18, 2017 17:57
Uma urna contém 8 bolas brancas e 6 bolas pretas. Ao serem retiradas, ao acaso, 4 bolas da urna, sem reposição, a probabilidade de que pelo menos três bolas sejam pretas é igual a:
a) 25/143
b) 23/77
c)18/57
d) 31/65
e)48/91
-
pribl17-
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Ago 18, 2017 17:03
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielFerreira » Dom Ago 20, 2017 02:34
por DanielFerreira » Dom Ago 20, 2017 02:34
pribl17- escreveu:Uma urna contém 8 bolas brancas e 6 bolas pretas. Ao serem retiradas, ao acaso, 4 bolas da urna, sem reposição, a probabilidade de que pelo menos três bolas sejam pretas é igual a:
a) 25/143
b) 23/77
c)18/57
d) 31/65
e)48/91
Olá
pribl17, seja bem-vindo!!
Inicialmente, devemos determinar a quantidade de combinações com as bolas da urna. Dessa forma, teremos o espaço amostral (em quantidade). E, fazemos isso aplicando o conceito de
Combinação Simples. Segue,
Decisão: combinar 14 (8 + 6) bolas da urna de quatro em quatro.
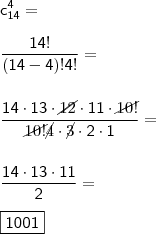
Por conseguinte,dividimos a resolução em dois casos: com três bolas retiradas e com quatro bolas retiradas.
CASO I:
d_1: combinar 6 bolas pretas tomadas três a três;
d_2: combinar 8 bolas que não são pretas tomadas uma a uma.
Então,
 CASO II
CASO II:
d_1: combinar 6 bolas pretas tomadas quatro a quatro;
Daí,
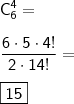
Pelo princípio aditivo,
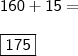
Por fim, aplicamos a definição de
probabilidade:
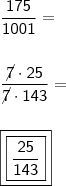
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de Probabilidade
por Bira » Ter Ago 07, 2012 17:43
- 0 Respostas
- 1074 Exibições
- Última mensagem por Bira

Ter Ago 07, 2012 17:43
Probabilidade
-
- Questão de probabilidade
por marinalcd » Dom Out 14, 2012 21:50
- 2 Respostas
- 1667 Exibições
- Última mensagem por MarceloFantini

Seg Out 15, 2012 00:46
Probabilidade
-
- questão probabilidade
por felipe-santiago » Qua Nov 28, 2012 23:59
- 4 Respostas
- 2308 Exibições
- Última mensagem por felipe-santiago

Qui Nov 29, 2012 16:37
Probabilidade
-
- Questão de probabilidade
por amanda s » Sex Nov 15, 2013 15:06
- 0 Respostas
- 982 Exibições
- Última mensagem por amanda s

Sex Nov 15, 2013 15:06
Probabilidade
-
- [probabilidade] questão
por amanda s » Sex Nov 15, 2013 20:18
- 0 Respostas
- 909 Exibições
- Última mensagem por amanda s

Sex Nov 15, 2013 20:18
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



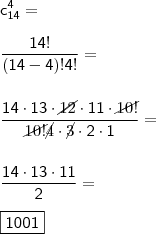

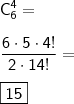
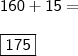
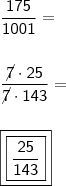

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
