Poderia alguém me dizer como chegar na fórmula da soma:
Sn=1^2 + 2^2 + ... + n^2 = (n(n+1)(2n+1))/6
Agradeço!




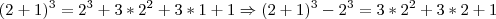
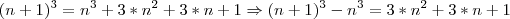
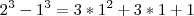
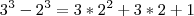
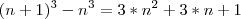
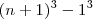 .
.
 , e logo,
, e logo,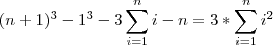 . Desenvolvendo,
. Desenvolvendo,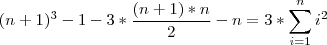 .
.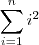
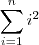 =
=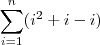
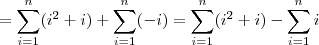
![=\sum_{i=1}^{n}[i(i+1)]-\sum_{i=1}^{n}i =\sum_{i=1}^{n}[i(i+1)]-\sum_{i=1}^{n}i](/latexrender/pictures/b4b53afde0b777c1081c856007d27994.png)

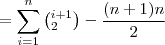
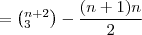

Voltar para Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.