-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478864 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536307 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499979 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 718737 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2144369 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Pessoa Estranha » Ter Dez 17, 2013 22:35
por Pessoa Estranha » Ter Dez 17, 2013 22:35
"SE A E B SÃO CONJUNTOS E A
QUANTIDADE DE ELEMENTOS EM A É n E A
EM B É r, QUANTAS FUNÇÕES f : A ----> B, INJETORAS EXISTEM ?
(

) "
Por favor, não quero a resolução e nem mesmo decorar fórmulas. Quero entender a questão. Quando tentei resolver, deu errado. Por favor, ajudem....
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 17:59
por e8group » Qua Dez 18, 2013 17:59
Veja um exemplo para

e

. Considere
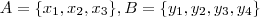
e seja

o conjunto das aplicações

injetoras .Notando que
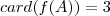
,poderíamos pensar em quantos subconjuntos (distintos) de

possui cardinalidade 3 . Nota :
Para cada subconjunto
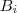
de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que
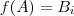
.
Obs.:
Em relação as apliçaões
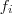
cuja o conjunto imagem é
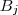
, o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect.

o que difere estas funções são os conjuntos imagens .
Exemplo :
Seja
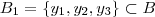
. É possível definir

aplicações injetivas (distintas) . Ora , se
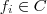
podemos ter
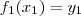
ou

ou ainda
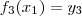
.Assim , basta por

(j=1,2,3) .
Mas ainda há outros subconjuntos de B ,

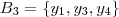
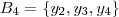
.
(Note que o número de subconjuntos com cardinalidade = 3 pode ser calculado por
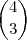
).
Logo , ao todo é possível definir 12 aplicações

injetivas (distintas) , em linguagem de conjunto

.
O que acha ? Caso esteja correto ,dá para generalizar utilizando o raciocínio acima ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por tenebroso » Qua Dez 18, 2013 18:34
por tenebroso » Qua Dez 18, 2013 18:34
ALGUÉM PODERIA DAR UMA AJUDINHA LÁ EM MINHAS QUESTÕES...? EHHEHEHEHE..

-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 20:51
por e8group » Qua Dez 18, 2013 20:51
Não está certo .
Por exemplo ,considere
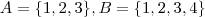
. E defina

injetora . Segue-se que
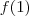
pode tomar 4 valores ,
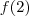
pode tomar 3 valores e
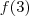
2 valores . Assim o número total de funções injetivas é

.
Justificativa .
Defina
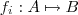
injetora .
Como vimos
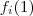
pode tomar 4 valores ,suponha

.Então
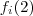
pode tomar um dos 4 valores exceto m ,suponha

e
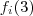
pode tomar um dos 4 valores exceto
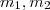
, suponha
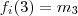
. Estas palavras acima se resume em :
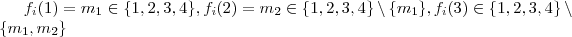
.
Imagine 3 segmentos de retas verticais
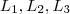
.Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante )
Partindo do primeiro ponto de
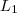
e escolhendo um caminho dentre os

que há para chegar em um dos pontos de
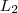
.Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de
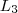
dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,
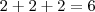
aplicações injetoras .
Partindo do segundo ponto de
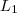
e fazendo o mesmo acima obteremos
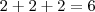
aplicações injetoras e assim por diante podemos obter no total
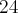
aplicações injetoras .
Acho que agora está certo .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Pessoa Estranha » Qua Dez 18, 2013 21:16
por Pessoa Estranha » Qua Dez 18, 2013 21:16
Eu ia questionar exatamente isto. Fiz as contas e, realmente, resultou em 24 e não em 12. Bem, com relação ao caso geral, n e m, vou pensar um pouco mais no que você escreveu e tentar fixar melhor a ideia. Muito obrigada pela ajuda!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 22:47
por e8group » Qua Dez 18, 2013 22:47
Anexei uma imagem neste tópico explicando este processo .
viewtopic.php?p=44888#p44888
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por tenebroso » Qua Dez 18, 2013 22:54
por tenebroso » Qua Dez 18, 2013 22:54
O lucro obtido por um comerciante na venda de determinado produto é dado , em reais, pela função L(x)= -1/10x²+ 15x, sendo x o número de unidades vendidas e o menor que x menor que 150.
Se L(m) é o lucro máximo que comerciante tem condições de obter, pode-se afirmar que log( l(m)/3m) é igual a:
a) 1+2log2
b) 2log2+log5
c) 2-log5 QUEM CONSEGUE RESOLVER? EU NÃO CONSEGUI, ALGUÉM CONSEGUE?
d) 1-2log2
e) 1-2log5
-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por Pessoa Estranha » Qui Dez 19, 2013 08:54
por Pessoa Estranha » Qui Dez 19, 2013 08:54
Olá....
Então, acho que podemos afirmar algo sobre o caso geral. Temos que, se A tem n elementos e B tem r, então, para f : A ----> B, podemos ter o seguinte raciocínio: seja x1 um elemento de A; x1 tem r elementos de B disponíveis para ser sua imagem. Mas, uma vez escolhido um r1 de B, como f deve ser injetora, outro elemento de A, um x2, já não tem mais r opções de imagem e, sim r-1. E isto se repete sucessivamente. Se aplicarmos este raciocínio, teríamos, para um caso geral, r.(r-1).(r-2). ... .(r-(n-1)). Bem, fazendo manipulações algébricas, chega-se à fórmula do Arranjo Ar,n =
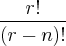
.
Fórmulas, fórmulas, fórmulas e mais fórmulas !!!!
Quando fiz este exercício pela primeira vez, consegui chegar até r.(r-1).(r-2). ... .(r-(n-1)) (e a resposta, é claro, não estava assim), mas nem passou pelo meu raciocínio que era, na verdade, a fórmula do arranjo.
Bem, muito obrigada pela sua ajuda. Consegui fixar melhor o raciocínio. Valeu!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Pessoa Estranha » Qui Dez 19, 2013 09:00
por Pessoa Estranha » Qui Dez 19, 2013 09:00
Tenebroso, você tentou resolver o seu exercício ou tem alguma ideia ? Se, até amanhã, ninguém te ajudar, tentarei fazer. Estou olhando os seus exercícios. Aquele de
combinatória está bem esquisito, parece que falta informação. Até mais.

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Análise combinatória [exercício]
por Valdemir Oliveira » Sáb Fev 09, 2013 01:23
- 4 Respostas
- 2634 Exibições
- Última mensagem por Valdemir Oliveira

Sáb Fev 09, 2013 21:28
Análise Combinatória
-
- [Analise combinatoria] exercicio
por amanda s » Sex Nov 15, 2013 20:17
- 0 Respostas
- 795 Exibições
- Última mensagem por amanda s

Sex Nov 15, 2013 20:17
Análise Combinatória
-
- [Análise Combinatória] Exercício
por Pessoa Estranha » Qua Dez 11, 2013 17:40
- 1 Respostas
- 1019 Exibições
- Última mensagem por Pessoa Estranha

Qui Dez 12, 2013 20:55
Análise Combinatória
-
- [Análise Combinatória] Exercício
por Pessoa Estranha » Ter Dez 17, 2013 22:27
- 0 Respostas
- 1364 Exibições
- Última mensagem por Pessoa Estranha

Ter Dez 17, 2013 22:27
Análise Combinatória
-
- Análise Combinatória - Dúvida em exercício
por carlosvinnicius » Ter Fev 08, 2011 23:01
- 1 Respostas
- 2876 Exibições
- Última mensagem por MarceloFantini

Ter Fev 08, 2011 23:30
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 16 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ) "
) "
 ) "
) "
 e
e  . Considere
. Considere 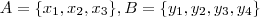 e seja
e seja  o conjunto das aplicações
o conjunto das aplicações injetoras .Notando que
injetoras .Notando que 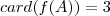 ,poderíamos pensar em quantos subconjuntos (distintos) de
,poderíamos pensar em quantos subconjuntos (distintos) de  possui cardinalidade 3 . Nota :
possui cardinalidade 3 . Nota : 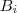 de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que
de B com 3 elementos é possível obter o mesmo número de aplicações injetivas tais que 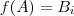 .
. 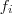 cuja o conjunto imagem é
cuja o conjunto imagem é 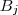 , o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect.
, o que difere cada aplicação é a regra de associação . E a cada par de aplicações cujos conjuntos imagens são respect.  o que difere estas funções são os conjuntos imagens .
o que difere estas funções são os conjuntos imagens . 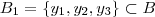 . É possível definir
. É possível definir  aplicações injetivas (distintas) . Ora , se
aplicações injetivas (distintas) . Ora , se 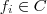 podemos ter
podemos ter 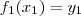 ou
ou  ou ainda
ou ainda 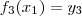 .Assim , basta por
.Assim , basta por  (j=1,2,3) .
(j=1,2,3) . 
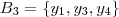
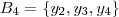 .
.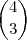 ).
). injetivas (distintas) , em linguagem de conjunto
injetivas (distintas) , em linguagem de conjunto  .
. 

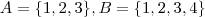 . E defina
. E defina  injetora . Segue-se que
injetora . Segue-se que 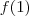 pode tomar 4 valores ,
pode tomar 4 valores , 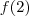 pode tomar 3 valores e
pode tomar 3 valores e 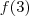 2 valores . Assim o número total de funções injetivas é
2 valores . Assim o número total de funções injetivas é  .
. 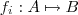 injetora .
injetora . 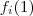 pode tomar 4 valores ,suponha
pode tomar 4 valores ,suponha  .Então
.Então 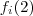 pode tomar um dos 4 valores exceto m ,suponha
pode tomar um dos 4 valores exceto m ,suponha  e
e 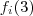 pode tomar um dos 4 valores exceto
pode tomar um dos 4 valores exceto 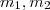 , suponha
, suponha 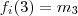 . Estas palavras acima se resume em :
. Estas palavras acima se resume em : 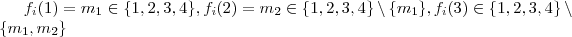 .
.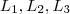 .Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante )
.Marque 4 pontos sobre L_1 , 3 pontos sobre a reta L_2 e 2 sobre a L_3 (em que estes pontos podem ser visto com os valores que m_i podem assumir ,escolhendo um na primeira reta ,na segunda reta terá 3 possibilidades todas distintas da escolha anterior e assim por diante )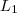 e escolhendo um caminho dentre os
e escolhendo um caminho dentre os  que há para chegar em um dos pontos de
que há para chegar em um dos pontos de 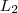 .Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de
.Chegando lá , podemos escolher um caminho p/ chegar em um dos pontos de 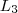 dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos ,
dentre os 3 disponíveis . Para cada procedimento completo nos fornecerá uma aplicação injetiva .Só aqui já conseguimos , 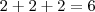 aplicações injetoras .
aplicações injetoras . 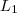 e fazendo o mesmo acima obteremos
e fazendo o mesmo acima obteremos 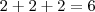 aplicações injetoras e assim por diante podemos obter no total
aplicações injetoras e assim por diante podemos obter no total 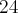 aplicações injetoras .
aplicações injetoras .




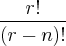 .
.





 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
