neste caso então 2.4=8 então 14-8=6, sendo assim temos que distribuir 6 moedas entre oito pessoas
podemos ter as moedas sepradas em grupos, com quantidades diferentes de moedas,1,2,3,4,5,6
1 caso: 1 1 1 1 1 1=seis grupos iguais
2 caso: 2 1 1 1 1=4 gupos iguais e 1 diferente
3 caso: 2 2 1 1= 2 grupos diferentes
4 caso: 2 2 2 = 3 grupos igauis
5 caso: 3 1 1 1 = 3 grupos igauis e 1 diferente
6 caso: 3 2 1= 3 grupos diferentes
7 caso: 3 3 = 2 grupos iguais
8 caso: 4 1 1 = 2 grupos igauis e 1 diferente
9 caso: 4 2 = 2 gruos diferentes
10 caso: 5 1 = dois grupos dierentes
11 caso: 6 = 1 grupos
se os grupos são igauis eu tenho que fazer a combinação deles com o numero de pessoas, se são diferentes tenho que fazer o arranjo deles
1 caso:
no primeiro caso seis grupos iguais

2 caso
no segundo caso pro primeiro grupo eu tenho 9 possibilidades, então sobram 8 possiblidades para os 4 outros grupos sendo que eu tenho que fazer a combinação deles em oito pois os grupos sao iguais
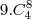
3 caso
para os dois primeiros grupos eu tenho que fazer a combinação deles em 9 e para os outros 2 grupos sobrma 7 possibilidades para que eles sejam combinadas entre elas
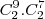
4 caso:
para o proximo como os grupos são iguais eu tres grupos distribuido em 9 pessoas
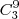
5 caso:
para o grupo de 3 eu tenho a possivilidade de 9 pessoas, para os outro 3 grupos restam a possivilidade de 8 pessoas sendo que eu devo fazer a combinação deles entre essas 8 pessoas
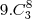
6 caso:
no proximo caso eu tenho tres grupos diferentes então as possibilidades são
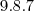
7 caso:
neste caso eu tenho que são dois grupos diferentes para 9 pessoas então é simplesmente a combinação

8 caso:
para este caso para o grupo diferente eu tenho 9 possibilidade de pessoas, para os outros dois grupos que são iguais eu posso combina-los entre 8 pessoas então
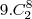
9 caso:
neste caso eu tenho simplesmente a combinação de 2 grupos diferentes entre 9 pessoas
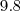
10 caso:
neste caso tambem tenho a combinação de 2 grupos diferentes entre 9 pessoas
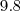
11 caso:
neste caso tenho apenas um grupo que tem a possibilidade de 9 pessoas
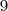
a soma dos 11 casos vai dar o total de possibilidades
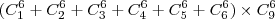
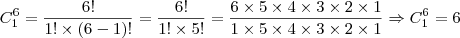
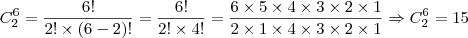
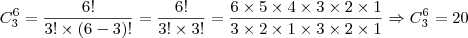
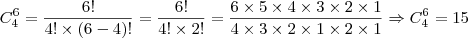
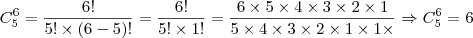
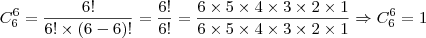
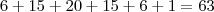
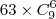 , tenho problema ao tentar encontrar
, tenho problema ao tentar encontrar  , pois
, pois 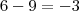 , então não consigo resolver. como eu devo fazer?
, então não consigo resolver. como eu devo fazer?

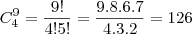

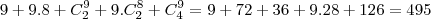

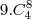
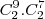
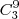
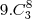
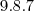

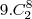
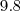
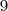

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)