Em um projeto de visita a escolas do batalhão, estão envolvidos três sargentos e dez soldados. Para uma visita, é formado um grupo com um sargento e três soldados; porém, devido às atividades do quartel, os soldados Araújo e Batista não poderão estar no mesmo grupo. Dessa forma, determine de quantas maneiras distintas pode-se formar esse grupo.
A) 24
B) 32
C) 132
D) 216
O que eu tentei:
(1)
Primeiro, fiz a combinação sem considerar a regra (Araújo e Batista no mesmo grupo), encontrando o máximo de combinações possíveis:
Entre os soldados:
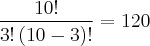
Segundo passo: calculei o número de combinações em que Araújo e Batista ficariam no mesmo grupo:
Entre os soldados:

Considerando apenas os soldados, a diferença entre o total de possibilidades e as possibilidades em que ambos os soldados estão no mesmo grupo resulta em:

Considerando a combinação entre os sargentos e soldados:
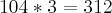
(2)
Considerei que Araújo e Batista fossem uma única pessoa:

Considerando a combinação entre os sargentos e soldados:

-
Tendo em vista os resultados, ambos não estão entre as alternativas. Se alguém puder esclarecer esta questão, ficarei grato.


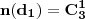 ;
;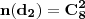
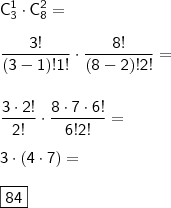
 .
. 
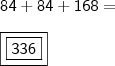

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.