Oito amigos, quatro homens e quatro mulheres, decidiram começar um jogo de tabuleiro e precisavam se organizar em três times: dois trios e uma dupla, sendo que nenhum time poderia ser formado apenas por homens ou apenas por mulheres. De quantas maneiras os times poderiam ser formados?
a. 144
b. 360
c. 720
d. 2.160
e. 2.880
Tentativas:
Identifiquei que era um problema de combinação. Fiz as possibilidade de cada trio, considerando C 8,3 + C 8,3 + C 8,2 (se multiplicasse iria dar um resultado absurdo). Depois fiz as exceções C 4,3 x 2 + C 4,2. Desse segundo resultado diminui do resultado da primeira combinação.
Como cheguei a um resultado longe de todas as opções da questão, vi que meu raciocínio estava errado, mas não sei bem onde.
Podem me ajudar?
Obrigada!


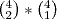
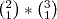
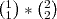

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)