 por na7777 » Sex Mar 07, 2014 09:26
por na7777 » Sex Mar 07, 2014 09:26
Bom dia, tentei diversas vezes chegar ao gabarito desta questão abaixo e não consegui. Tentei seguir o principio fundamental da contagem e tentei a fórmula da combinação. Como faz essa questão? Por favor! Me ajude, vou tentar esse concurso. Terminei o ensino médio há muito tempo, não me lembro. Muito Obrigada.
(Questão Concurso EPE 2012)
Dois adultos e seis crianças aguardavam um táxi.
Quando o táxi chegou, o motorista informou-lhes que o carro
só pode transportar 5 pessoas e, portanto, só poderiam
viajar ele, o motorista, e mais 4 passageiros. Os adultos
decidiram que um deles embarcaria no táxi, levando con-
sigo o maior número possível de crianças, e que o outro
ficaria com as crianças restantes, aguardando outro táxi.
De quantos modos distintos é possível escolher os passa-
geiros que embarcarão nesse táxi?
-
na7777
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mar 07, 2014 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: gestão de recursos humanos
- Andamento: cursando
 por fff » Sex Mar 07, 2014 17:02
por fff » Sex Mar 07, 2014 17:02
Boa tarde.
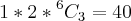
1-O motorista é fixo
2- escolher 1 de 2 adultos
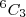
-maneiras de repartir as 6 crianças pelos 3 lugares restantes.
-

fff
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sáb Dez 21, 2013 11:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Informática
- Andamento: cursando
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16390 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12560 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8482 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7935 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6631 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


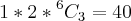
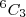 -maneiras de repartir as 6 crianças pelos 3 lugares restantes.
-maneiras de repartir as 6 crianças pelos 3 lugares restantes.
