[Análise combinatória] Seleção

por **Lidstew** » Ter Abr 16, 2013 15:32

Alguém poderia me explicar como fazer esta questão ?
Cada seleção participante da copa do mundo de futebol inscreve 23 jogadores, sendo necessariamente três goleiros. Em cada partida, dois jogadores de cada seleção são escolhidos entre os 23 inscritos para o exame anti-doping, mas são descartadas as possibilidades de que os dois jogadores escolhidos sejam goleiros. De quantas maneiras diferentes estes dois jogadores podem ser escolhidos?
Fiz no meu teste do colégio e deu 190, o prof disse que tava errado e há um mês peço a ele explicação pra esta questão e ele só enrola... rs Obrigada pra quem ajudar!

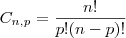
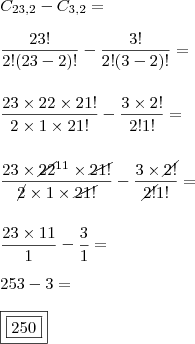
por **young_jedi** » Ter Abr 16, 2013 16:07

os dois não podem ser goleiros mais um deles pode
então o total de possibilidades sera
o total de combinção de dois jogadores em 23 menos o numero de combinação de 2 goleiro em tres

$C_{(2,23)}-C_{(2,3)}=253-3=250$

por **DanielFerreira** » Ter Abr 16, 2013 16:13

Lidstew,
pensei da seguinte forma:

- a ordem não é importante; imaginemos que sejam escolhidos um atacante e um zagueiro respectivamente, se trocarmos a ordem (zagueiro e atacante) nada mudará, portanto, temos uma combinação;

- não é admissível dois goleiros, mas um goleiro e um atacante, por exemplo, sim;

Com isso, podemos encontrar a quantidade total de combinações e subtrair das combinações feitas apenas com os goleiros.

onde, $C_{n, p} = \frac{n!}{p!(n - p)!}$

Segue que,

$\\ C_{23, 2} - C_{3, 2} = \\\\ \frac{23!}{2!(23 - 2)!} - \frac{3!}{2!(3 - 2)!} = \\\\\\ \frac{23 \times 22 \times 21!}{2 \times 1 \times 21!} - \frac{3 \times 2!}{2! 1!} = \\\\\\ \frac{23 \times \cancel{22}^{11} \times \cancel{21!}}{\cancel{2} \times 1 \times \cancel{21!}} - \frac{3 \times \cancel{2!}}{\cancel{2!} 1!} = \\\\\\ \frac{23 \times 11}{1} - \frac{3}{1} = \\\\ 253 - 3 = \\\\ \boxed{\boxed{250}}$

Att,

Daniel.

[Análise combinatória] Seleção

[Análise combinatória] Seleção

[Análise combinatória] Seleção

Re: [Análise combinatória] Seleção

Re: [Análise combinatória] Seleção

Quem está online