Olá, pessoal!
Estou com problemas para chegar ao resultado do seguinte exercício:
(Caderno de Exercícios - Anglo)
43. Considere os anagramas da palavra CAMARADA.
c) Quantos possuem as consoantes C, M, D e R juntas e nesta ordem? (Resposta: 5)
d) Quantos possuem as vogais juntas? (Resposta: 120)
Obrigada.






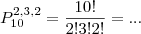
 é a quantidade de vezes que uma mesma letra se repete, no caso de VIVA, 2 é a quantidade de V's; no segundo exemplo:
é a quantidade de vezes que uma mesma letra se repete, no caso de VIVA, 2 é a quantidade de V's; no segundo exemplo:
 .
.



