 por Ed_29 » Qui Ago 09, 2012 21:42
por Ed_29 » Qui Ago 09, 2012 21:42
Três rapases e duas moças vão ao cinema e desejam sentar-se,os cinco,lado a lado, na mesma fila. O número de maneiras pelas quais eles podem distribuir-se nos assentos de modo que as duas moças fiquem juntas, uma ao lado da outra, é igual a
a)2
b)4
c)24
d)48
e)120
pessoal não consegui resolver. alguém sabe?
-
Ed_29
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Ago 06, 2012 18:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em química
- Andamento: formado
 por fraol » Sex Ago 10, 2012 12:12
por fraol » Sex Ago 10, 2012 12:12
Bom dia,
Uma questão que tem um modelo de solução semelhante está em
Dificil questao de probabilidade.
Você pode usar o mesmo raciocínio:
1) Coloque as duas moças em uma poltrona (gde) só. Logo você vai permutar 4 lugares =
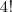
.
2) As duas moças também podem trocar de lugar entre si, logo

permutações.
Para responder basta multiplicar 1) e 2) acima.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Ed_29 » Sáb Ago 11, 2012 14:46
por Ed_29 » Sáb Ago 11, 2012 14:46
fraol escreveu:Bom dia,
Uma questão que tem um modelo de solução semelhante está em
Dificil questao de probabilidade.
Você pode usar o mesmo raciocínio:
1) Coloque as duas moças em uma poltrona (gde) só. Logo você vai permutar 4 lugares =
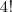
.
2) As duas moças também podem trocar de lugar entre si, logo

permutações.
Para responder basta multiplicar 1) e 2) acima.
.
Boa tarde!
não entendi a 1º colocação?
1) Coloque as duas moças em uma poltrona (gde) só. Logo você vai permutar 4 lugares =
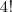
-
Ed_29
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Ago 06, 2012 18:21
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em química
- Andamento: formado
 por fraol » Sáb Ago 11, 2012 15:24
por fraol » Sáb Ago 11, 2012 15:24
Boa tarde,
não entendi a 1º colocação?
1) Coloque as duas moças em uma poltrona (gde) só. Logo você vai permutar 4 lugares =
Bom como são cinco pessoas sendo duas moças que devem permanecer juntas, fazemos de conta que elas estão grudadas, sentadas juntas. Assim você deve permutar, trocar, 4 posições, as tais 4! permutações. Como as duas moças que estão juntas também podem intercambiar seus lugares, temos 2! = 2 permutações delas. Aplicando o princípio multiplicativo => 4! . 2! .
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Combinatória-analise combinatoria
por heloisacarvalho83 » Seg Fev 27, 2012 22:40
- 1 Respostas
- 2887 Exibições
- Última mensagem por Livia000

Qua Mai 23, 2012 00:26
Estatística
-
- combinatória
por Adilson » Sex Ago 28, 2009 13:50
- 1 Respostas
- 2142 Exibições
- Última mensagem por Molina

Sex Ago 28, 2009 21:19
Estatística
-
- Combinatória
por 2137RF » Sex Out 09, 2009 11:25
- 4 Respostas
- 3475 Exibições
- Última mensagem por shirata

Qui Nov 26, 2009 06:38
Estatística
-
- combinatória
por apoliveirarj » Dom Jul 25, 2010 16:50
- 2 Respostas
- 4877 Exibições
- Última mensagem por apoliveirarj

Qui Ago 05, 2010 19:27
Estatística
-
- Combinatória
por apoliveirarj » Sáb Ago 07, 2010 12:23
- 2 Respostas
- 2465 Exibições
- Última mensagem por apoliveirarj

Sex Ago 13, 2010 15:55
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


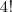 .
. permutações.
permutações.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
