Numa escola de Salvador 56 alunos lêem o jornal A, 21 lêem os jornais A e B, 106 lêem apenas um dos jornais e 66 não lêem o jornal B. Quantos alunos estudam na escola?
Resposta > 158 alunos
Provavelmente é de fácil solução para vocês, mas não consigo chegar no resultado, pois simplesmente no Diagrama de Venn não sei onde coloco os 106 alunos e os 66 alunos, estou frustrado por não saber resolver esta questão, me ajudem.
Obrigado.
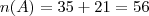
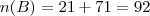
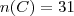
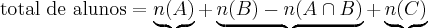
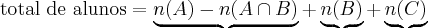
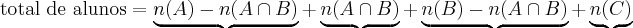
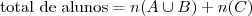
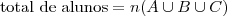
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)