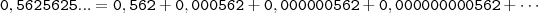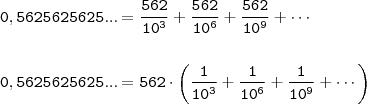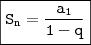-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478753 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 535182 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498769 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 715402 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2138556 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por creberson » Sex Mai 24, 2019 11:03
por creberson » Sex Mai 24, 2019 11:03
Ola tudo bem ?
Estou com duvida para transformar em fração geratriz nessa caso
2,36161616
X=2,3631616
multiplico por 10 a equação depois por mil que resultara 2338/990
nesse caso aqui é que tenho duvidas 0,5625625 como faço?
Creberson
Itapirapuã Paulista
-
creberson
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Jul 23, 2012 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matematica
- Andamento: cursando
 por DanielFerreira » Qui Set 12, 2019 23:19
por DanielFerreira » Qui Set 12, 2019 23:19
Creberson, note que:
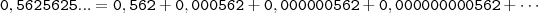
Noutras 'palavras',
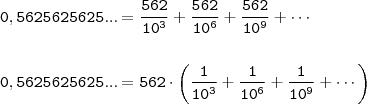
Como podemos observar, os termos entre parênteses é uma
sequência conhecida -
Progressão Geométrica!!
Lembre-se que a soma dos termos de uma
PG infinita é dada por:
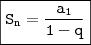
Resta concluir!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.G. Dízima Periódica
por Rafael16 » Qua Jul 18, 2012 19:48
- 3 Respostas
- 7900 Exibições
- Última mensagem por Russman

Qua Jul 18, 2012 21:20
Progressões
-
- IME-96 Função periódica
por Balanar » Sáb Ago 07, 2010 17:58
- 4 Respostas
- 10557 Exibições
- Última mensagem por kamillanjb

Ter Mar 15, 2011 22:57
Desafios Difíceis
-
- Dízima
por Cristina Lins » Qui Abr 06, 2017 10:47
- 0 Respostas
- 7085 Exibições
- Última mensagem por Cristina Lins

Qui Abr 06, 2017 10:47
Álgebra Elementar
-
- [Sequência convergente e periódica ] Prove ...
por e8group » Seg Jan 20, 2014 23:45
- 0 Respostas
- 8271 Exibições
- Última mensagem por e8group

Seg Jan 20, 2014 23:45
Sequências
-
- Encontre a fração geratriz da dizima 1,777....
por andersontricordiano » Qua Abr 13, 2011 22:07
- 1 Respostas
- 9245 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:21
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.