-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480696 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542269 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 505963 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 734807 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2180571 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por CarolineCecy » Sex Abr 14, 2017 03:30
por CarolineCecy » Sex Abr 14, 2017 03:30
Sobre as propriedades que tornam o conjunto dos números Reais um "corpo ordenado", gostaria de saber se a "Compatibilidade da ordem com a multiplicação", expressa como: "se x?y e 0?z, então x.z?y.z" (tomando x, y e z como números Reais), também pode ser expressa como: "se x<y e z<0, então x.z>y.z" ou se esta última sentença constitui outra propriedade, e qual seria? Ps: É uma questão de "nomenclatura" mesmo, digamos assim, preciso NOMEAR esta propriedade da última sentença que digitei, e não necessariamente demonstrar.
-
CarolineCecy
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 14, 2017 02:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- conjunto dos números reais
por jose henrique » Sex Set 03, 2010 21:58
- 1 Respostas
- 1877 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:05
Álgebra Elementar
-
- conjunto de numeros reais
por VERONICALIMA » Sex Nov 29, 2013 16:23
- 1 Respostas
- 1463 Exibições
- Última mensagem por DanielFerreira

Ter Fev 11, 2014 16:42
Conjuntos
-
- Conjunto dos números Reais
por CarolineCecy » Sex Abr 14, 2017 03:29
- 0 Respostas
- 2071 Exibições
- Última mensagem por CarolineCecy

Sex Abr 14, 2017 03:29
Conjuntos
-
- [Conjunto dos Numeros Reais] Abstrações e Comprovações
por rafaz182 » Qui Jan 29, 2015 13:03
- 2 Respostas
- 3256 Exibições
- Última mensagem por rafaz182

Ter Fev 03, 2015 10:26
Conjuntos
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1709 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



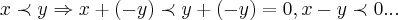 ,como
,como 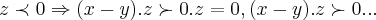 ,usando a propriedade distributiva da mulplicaçao,teremos:
,usando a propriedade distributiva da mulplicaçao,teremos: