-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478707 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534800 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498399 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714272 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2136624 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Almar » Qui Fev 04, 2010 15:33
por Almar » Qui Fev 04, 2010 15:33
Prezados,
Sou novo no fórum, gostaria que alguém pudesse me responder o que segue:
Em se tratatando de Conjuntos, provar das três formas abaixo listadas que a Operação "Diferença Simétrica" é associativa:

1. Provar por tabela verdade:
2. Provar por Diagrama de Venn:
3. Provar por algebra:
Aguardo respostas e desde já agradeço a todos.
Att.
Almar Santiago
Bacharelando em Ciências da Computação.
-
Almar
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Fev 04, 2010 15:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CIÊNCIAS DA COMPUTAÇÃO
- Andamento: cursando
 por diasbr » Qui Fev 04, 2010 20:49
por diasbr » Qui Fev 04, 2010 20:49
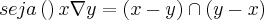
dai fica fácil
dica considere cada elemento como x-y como um conjunto e recorra à associativa do au(buc)
tabela dica escreva cada elemento
assim
três elementos = Combinatória 2x2x2=8 depois check se verdadeiro ou falso
a b c (a - c) a U b

depois de vc fazer isso tudo verifique a tautologia que vc deseja
o o o 0 0 0
o o 1 0 0 0
o 1 0 0 1 0
o 1 1 0 1 0
1 0 0 1 1 0
1 0 1 0 1 1
1 1 0 1 1 0
1 1 1 0 1 1
van é o desenho de círculos pinte eles e fica visual
-
diasbr
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Fev 03, 2010 21:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: engenharia
- Andamento: cursando
 por Incognite » Sáb Mar 10, 2018 19:27
por Incognite » Sáb Mar 10, 2018 19:27
diasbr escreveu: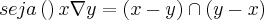
dai fica fácil
dica considere cada elemento como x-y como um conjunto e recorra à associativa do au(buc)
tabela dica escreva cada elemento
assim
três elementos = Combinatória 2x2x2=8 depois check se verdadeiro ou falso
a b c (a - c) a U b

depois de vc fazer isso tudo verifique a tautologia que vc deseja
o o o 0 0 0
o o 1 0 0 0
o 1 0 0 1 0
o 1 1 0 1 0
1 0 0 1 1 0
1 0 1 0 1 1
1 1 0 1 1 0
1 1 1 0 1 1
van é o desenho de círculos pinte eles e fica visual
Olá, estou com a mesma dúvida do postador do tópico. Como consigo provar algébricamente dessa forma que você disse?? Estou tentando há horas esse exercício, até agora nada
-
Incognite
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 10, 2018 18:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ciências biológicas
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Diferença simétrica
por Incognite » Sáb Mar 10, 2018 18:22
- 1 Respostas
- 2930 Exibições
- Última mensagem por adauto martins

Qui Abr 26, 2018 20:15
Conjuntos
-
- Endomorfismo e matriz anti simetrica
por matlearn » Dom Mar 20, 2011 23:40
- 0 Respostas
- 2239 Exibições
- Última mensagem por matlearn

Dom Mar 20, 2011 23:40
Geometria Analítica
-
- [Algebra Linear] Matriz Simetrica
por fabriel » Sex Mai 31, 2013 17:07
- 5 Respostas
- 5858 Exibições
- Última mensagem por Molina

Sex Mai 31, 2013 22:25
Álgebra Linear
-
- Diferença
por DanielFerreira » Sáb Set 26, 2009 12:10
- 4 Respostas
- 4696 Exibições
- Última mensagem por DanielFerreira

Ter Jun 08, 2010 18:19
Piadas
-
- A Diferença de g(t)-h(t)
por Rayane01 » Sex Mar 31, 2017 20:38
- 3 Respostas
- 6995 Exibições
- Última mensagem por Cleyson007

Sáb Abr 01, 2017 12:33
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



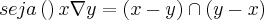
 depois de vc fazer isso tudo verifique a tautologia que vc deseja
depois de vc fazer isso tudo verifique a tautologia que vc deseja 

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.