Enunciado: Dados dois números x e y reais e positivos, chama-se média aritmética de x com y o real a=
 e chama-se média geométrica o real g=
e chama-se média geométrica o real g=![\sqrt[]{xy} \sqrt[]{xy}](/latexrender/pictures/73a3f5eb9b695f3c2c1b554a600498a8.png) . Mostre que a
. Mostre que a g para todos x , y
g para todos x , y
 positivo.
positivo.Eu comecei a responder da seguinte maneira: considerei um numero K, tal que k=xy. Ai fiz :


![\sqrt[]{xy} \sqrt[]{xy}](/latexrender/pictures/73a3f5eb9b695f3c2c1b554a600498a8.png) ----------------------
---------------------- 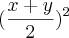

![({\sqrt[]{xy}})^{2} ({\sqrt[]{xy}})^{2}](/latexrender/pictures/e549db8f4d1c9c9f7de7c786769a14a6.png) ----------------
----------------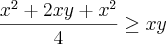 e como k=xy ficou
e como k=xy ficou  . Porém eu fiquei estagnado nessa parte, não sei se é porque minha solução esta errada ou por eu estar esquecendo algo ou não sei mais o que. O fato é que fiquei tentando resolver esse problema por mais ou menos 105 minutos até chegar nessa solução. Porém não sei se ela esta certa. Por favor, ajudem -me.
. Porém eu fiquei estagnado nessa parte, não sei se é porque minha solução esta errada ou por eu estar esquecendo algo ou não sei mais o que. O fato é que fiquei tentando resolver esse problema por mais ou menos 105 minutos até chegar nessa solução. Porém não sei se ela esta certa. Por favor, ajudem -me.

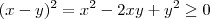 ;somando-se
;somando-se 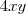 na desigualdade ,
na desigualdade ,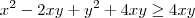 (que também é verdade) .
(que também é verdade) . 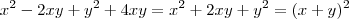 ,resulta
,resulta 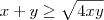 e portanto
e portanto 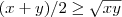


 .
.



