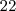jogadores de futebol convocados para um amistoso. Sabe-se que desses, 
são goleiros, 
podem jogar na defesa, podem jogar no meio de campo e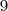 
podem jogar no ataque.Sabe-se também que
jogadores podem jogar na defesa e no meio,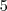 
jogadores podem jogar no meio ou no ataque e apenas 
jogador pode jogar na defesa e no ataque. Os goleiros só podem jogar no gol. Com base nas informações acima, responda:a) Quantos jogadores são tão versáteis que podem jogar na defesa, no meio e no ataque? 1
b) Quantos podem jogar apenas na defesa? 6
c) Quantos podem jogar apenas no ataque? 4
d) Quantos podem jogar no ataque ou no meio, mas nunca na defesa? 10
Por favor desenhe o Diagrama de Venn.
