Olá colegas...
Um trabalhador recebe R$ 510,00 em tíquetes alimentação, com valores de R$20,00 ou R$50,00 cada tíquete. O número de maneiras que pode ser formado o carnê de tíquetes é?
Tentei resolver assim:
1º tentativa
x = 20 e y = 50
x + y = 510
23.20 + 1.50 = 510
2º tentativa
x = 20 e y = 50
x + y = 510
3.20 + 9.50 = 510
assim por diante, percebi que é muito trabalhoso. Será que tem outra forma de chegar a resposta?
Desde já agradeço a ajuda. Abraços Lúcio


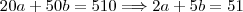
 e
e 
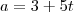 e
e 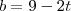 (sendo
(sendo 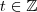 )
)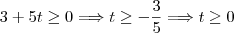
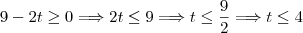
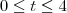
 maneiras.
maneiras.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)