 por binhavasconcellos » Sex Ago 10, 2012 10:25
por binhavasconcellos » Sex Ago 10, 2012 10:25
Após muitas discussões sobre alternativas viáveis de ações a serem implementadas,
visando à resolução de determinado problema, 145 membros de uma associação
comunitária de bairro votaram em duas propostas P1 e P2.
Se do total de votos se verificou que 48 foram favoráveis a P1, 54 foram favoráveis a P2
e 35 foram contrários às duas propostas, então o número de votos favoráveis às duas
propostas foi
01) 35 03) 48 05) 54
02) 43 04) 51
resp: 51
eu tentei por várias linhas de raciocínio ,e não achei o resultado .
-
binhavasconcellos
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Ago 10, 2012 10:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Ago 12, 2012 12:20
por DanielFerreira » Dom Ago 12, 2012 12:20
Oi
Binha,
seja bem vinda!
Consideremos que o número de votos favoráveis às duas propostas seja

, então:
- 54 foram favoráveis a
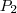
. Portanto, foram favoráveis
somente a
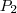
:

- 48 foram favoráveis a
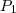
. Portanto, foram favoráveis
somente a
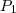
:

Daí,
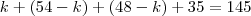
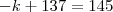

Esse valor não devia ser negativo, com isso, penso que há erro no enunciado; ou, minha
linha de raciocínio, também está errada! rsrssr
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Seg Ago 13, 2012 22:03
por DanielFerreira » Seg Ago 13, 2012 22:03
Binha,
boa noite!
Ainda não consegui ver erro na solução apresentada.
Vou analisar com mais calma, e amanhã retorno!
Até breve.
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Sex Ago 17, 2012 20:55
por DanielFerreira » Sex Ago 17, 2012 20:55
Binha,
desculpe, não consegui!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12994 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10976 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15117 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5034 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4803 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , então:
, então: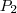 . Portanto, foram favoráveis
. Portanto, foram favoráveis 
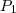 . Portanto, foram favoráveis
. Portanto, foram favoráveis 
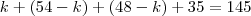
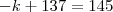



 .
.



