Um feirante possui uma Kombi para transportar caixas de frutas. Em uma viagem, ele consegue transportar no veículo 200 caixas de laranjas - caso transporte apenas laranjas - ou 300 caixas de tangerinas - caso transporte apenas tangerinas. O lucro por caixa de frutas é o seguinte: 20 unidades monetárias pelas laranjas, 30 unidades monetárias pelas tangerinas e 35 unidades monetárias pelas maçãs. De acordo com sua estimativa de vendas, o feirante decide transportar pelo menos 100 unidades de maçãs(Começa aqui, ele diz UNIDADE e não caixa). Considere a variável X1 como a quantidade vendida de caixas de maçãs, X2 a de caixas de laranjas e X3 a de caixas de tangerinas.
Questão 55 - A(s) inequação(ões) que representa(m) a(s) restrição (ões) de capacidade máxima de volume de transporte da Kombi é(são):
(A) X2 + X3 ? 5
(B) 3X2 + 2X3 ? 6
(C) X1 ? 100, X2 ? 200, X3 ? 300
(D) X2 ? 200, X3 ? 300
(E) X1 ? 200, X2 ? 300
Gabarito:B
Todo o problema é formulado ao redor de caixas e ele não fala quantas frutas cabe em uma cx, beleza, eu poderia usar como incognita para maçã por exemplo x¹=Q/100, sendo Q quantidade de frutas numa caixa que eu não sei, com isso minha função de maximização ficou:
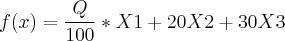
E eu paro por aqui pois não sei como resolver todas essas incognitas e muito menos como ele chegou ao resultado. Se alguém poder me ajudar agradeço, pois acho que essa questão esta errada tenho até amanha 08/04 para pedir recurso.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.