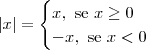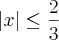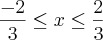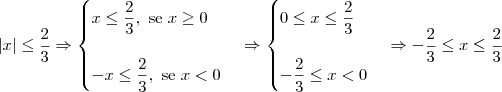Rafael16 escreveu:Resolvi essa equação:
2|x|² + 3|x| = 2
2|x|² = -3|x| + 2 --> C.E: -3x + 2 ? 0 ? x ? 2/3
A condição de existência está errada. O correto seria:

Ou seja, você escreveu -3x ao invés de -3|x|.
Resolvendo a condição de existência, temos que:

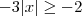
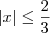
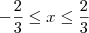
Rafael16 escreveu:2x² = -3x + 2
2x² + 3x - 2 = 0
Tirei a raiz e obtive 1/2 e -2. Como -2 é menor que 2/3, que é a condição de existência, sobrou só 1/2 que satisfaz a C.E. Portanto,
S = {1/2}. Mas a solução correta é S = {1/2, -1/2}.
Aqui há outro erro. Você tinha a equação:
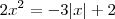
A partir daí, você simplesmente (sem qualquer motivo para isso) substituiu |x| por x. Então você escreveu:
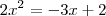
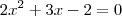
O erro desse raciocínio está no fato de que |x| não é igual a x.
Isso só é verdade quando

. No caso de x < 0, temos que |x| é igual a -x.
Rafael16 escreveu:E vi a resolução desse exercício logo abaixo mas não entendi:
2|x|² + 3|x| = 2
2|x|² + 3|x| - 2 = 0
para x < 0:
2x² - 3x - 2 = 0
raízes -> x = - 1/2 ou x = 2 ( não convém pois estamos supondo x < 0 )
para x >= 0 :
2x² + 3x - 2 = 0
raízes -> x = 1/2 ou x = - 2 ( não convém pois estamos supondo x >= 0 )
logo:
S = [ - 1/2 , 1/2 }
Não entendi esse "não convém", e também não entendi o porque o 2 não está no conjunto solução, pois é maior que C.E que é 2/3.
Aqui foi aplicado a definição de módulo:
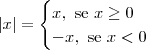
Dessa forma, a solução foi separada em dois casos: quando quando x < 0 e quando

.
O termo "não convém" é o mesmo que "não serve".
No primeiro caso, considerou-se que x < 0.
Ao resolver a equação, determinou-se que x = -1/2 e x = 2.
Ora, mas como considerou-se que x < 0, a solução x = 2 "não serve" (ou "não convém").
Já no segundo caso, quando considerou-se que

, determinou-se que x = 1/2 e x = -2.
Ora, mas como considerou-se que

, a solução x = -2 "não serve" (ou "não convém").



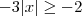
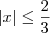
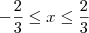
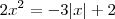
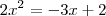
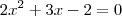
 . No caso de x < 0, temos que |x| é igual a -x.
. No caso de x < 0, temos que |x| é igual a -x.