 por Guidp09 » Qua Nov 18, 2020 16:49
por Guidp09 » Qua Nov 18, 2020 16:49
Boa tarde, pessoal. Tudo bem?
Gostaria de tirar uma dúvida...
96.000= X + 0,2X
1,2X= 96.000
X= 80.000
Nessa equação, não consigo visualizar como se chegou nesse valor de 1,2X. Tendo em vista a parte em negrito, gostaria de saber detalhadamente como chegou a esse resultado, pois tentei entender várias vezes e não consegui visualizar o por quê desse resultado (1,2X). Essa é uma equação feita através de uma questão de Contabilidade, pela banca CESPE. Se alguém puder me ajudar, agradeço desde já!
Abraço!
-
Guidp09
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Set 25, 2020 09:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Concurso
- Andamento: formado
 por DanielFerreira » Sex Nov 20, 2020 13:18
por DanielFerreira » Sex Nov 20, 2020 13:18
Olá
Guidp09, seja bem-vindo(a)!!
Comumente, o número UM não é exibido em termos algébricos. Com isso, quero dizer que
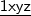
, por exemplo, é representado por
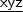
.
Dessa maneira,

é o mesmo que
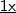
. Portanto,
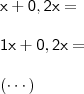
Qualquer dúvida, comente!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Guidp09 » Sex Nov 20, 2020 15:26
por Guidp09 » Sex Nov 20, 2020 15:26
Perfeito!!!
Entendi agora. Muito obrigado pela explicação, Daniela Ferreira. Tu é o cara!!!!! Me ajudou muito.
Abraço!

-
Guidp09
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Set 25, 2020 09:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Concurso
- Andamento: formado
 por DanielFerreira » Sex Nov 20, 2020 19:09
por DanielFerreira » Sex Nov 20, 2020 19:09
Não há de quê!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7721 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13219 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13019 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 6091 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8707 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


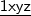 , por exemplo, é representado por
, por exemplo, é representado por 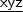 .
. é o mesmo que
é o mesmo que 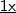 . Portanto,
. Portanto,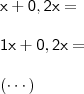



 , avisa que eu resolvo.
, avisa que eu resolvo.

