Equação Polinomial
Dada a equação 4x^4-ax^3+bx^2-cx+d=0 de raízes x1,x2;x3;x4, positivas tal que:x1/2+x2/4+x3/5+x4/8=1.Calcule a maior raiz.
a)1/2
b)1
c)2
d)7/3
e)5/4
r:c
a)1/2
b)1
c)2
d)7/3
e)5/4
r:c
AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!
http://www.ajudamatematica.com/
Flavio Cacequi escreveu:Dada a equação 4x^4-ax^3+bx^2-cx+d=0 de raízes x1,x2;x3;x4, positivas tal que:x1/2+x2/4+x3/5+x4/8=1.Calcule a maior raiz.
a)1/2
b)1
c)2
d)7/3
e)5/4
r:c
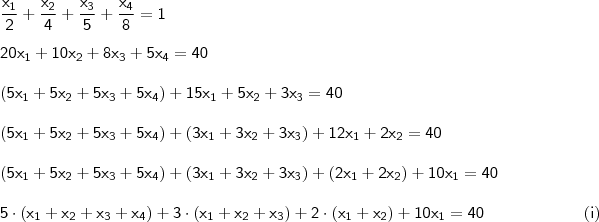
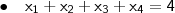
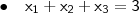

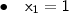
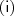 ,
,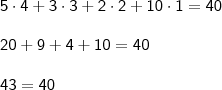
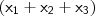 para 2, em vez de 3.
para 2, em vez de 3.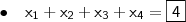
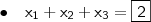
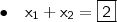

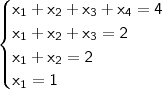
 , onde 1 tem multiplicidade dois!!
, onde 1 tem multiplicidade dois!!