-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480785 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 542807 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506559 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 736367 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2183827 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por ARCS » Seg Jul 31, 2017 17:34
por ARCS » Seg Jul 31, 2017 17:34
Preciso determinar uma função polinomial
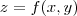
que satisfaça as seguintes condições:
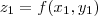
,
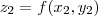
,
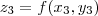
e

, em que
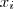
,
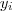
e
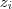
(para
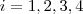
são valores prescritos.
Não conheço os métodos de interpolação de funções com duas variáveis, mas conheço os métodos de interpolação de funções com uma variável, tais como os métodos Vandermonde, Lagrange e Newton.
Os mencionados métodos podem ser estendidos para funções de duas variáveis ou existe algum método específico para interpolação de funções de duas variáveis?
-
ARCS
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Qui Out 28, 2010 18:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema com duas variáveis
por helen_chaves » Qua Jun 03, 2009 12:00
- 3 Respostas
- 3655 Exibições
- Última mensagem por Cleyson007

Sex Jun 05, 2009 12:51
Funções
-
- Limite de duas variaveis
por Tixa11 » Seg Abr 01, 2013 13:13
- 1 Respostas
- 1873 Exibições
- Última mensagem por young_jedi

Qua Abr 03, 2013 11:09
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Duas variaveis
por fabriel » Sáb Jun 15, 2013 16:48
- 2 Respostas
- 2142 Exibições
- Última mensagem por temujin

Sáb Jun 15, 2013 19:10
Cálculo: Limites, Derivadas e Integrais
-
- Função de duas variáveis
por lilianers » Qua Ago 21, 2013 19:37
- 1 Respostas
- 2011 Exibições
- Última mensagem por Renato_RJ

Qui Ago 22, 2013 12:46
Funções
-
- Limites duas variaveis
por Razoli » Qui Jul 03, 2014 23:22
- 2 Respostas
- 2164 Exibições
- Última mensagem por Razoli

Qui Jul 03, 2014 23:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
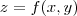 que satisfaça as seguintes condições:
que satisfaça as seguintes condições: 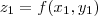 ,
, 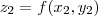 ,
, 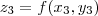 e
e  , em que
, em que 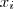 ,
,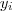 e
e 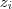 (para
(para 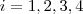 são valores prescritos.
são valores prescritos.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
