 por Marcones » Sáb Mar 21, 2015 11:37
por Marcones » Sáb Mar 21, 2015 11:37
Estou estudando a dias esse assunto de fatoração e só consegui resolver da questão 39 à 42
Semana inteira tentando, tentando, tentando, mas não estou conseguindo.

-
Marcones
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mar 21, 2015 11:10
- Formação Escolar: EJA
- Andamento: formado
 por Cleyson007 » Sáb Mar 21, 2015 12:13
por Cleyson007 » Sáb Mar 21, 2015 12:13
Bom dia Marcones!
Seja muito bem-vindo ao fórum.
Vamos primeiro ao exercício 45. Pode ser?
45)
x² - 4a² + 6x + 12a
Essa parte que deixei sublinhada para você é uma diferença de dois quadrados. Vamos resolvê-la por primeiro: (x - 2a)(x + 2a)
A outra parte pode ser resolvida por fator comum em evidência: 6(x + 2a)
Olha como está ficando: (x - 2a)(x + 2a) + 6(x + 2a)
Agora vamos fazer um agrupamento! Repare que o (x + 2a) aparece em ambos os lados. Logo,
(x + 2a) (x - 2a + 6)
Tente resolver algum outro exercício seguindo esses passos.
Qualquer dúvida estou a disposição

Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Marcones » Sáb Mar 21, 2015 14:16
por Marcones » Sáb Mar 21, 2015 14:16
Muito bem explicado! Esse eu já havia resolvido.
-
Marcones
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mar 21, 2015 11:10
- Formação Escolar: EJA
- Andamento: formado
 por Marcones » Sáb Mar 21, 2015 16:31
por Marcones » Sáb Mar 21, 2015 16:31
Me vê a 43, pode ser?
-
Marcones
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mar 21, 2015 11:10
- Formação Escolar: EJA
- Andamento: formado
 por Cleyson007 » Sáb Mar 21, 2015 18:13
por Cleyson007 » Sáb Mar 21, 2015 18:13

Lógico que sim!
Sabemos que
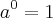
. Logo temos,
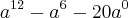
.
Colocando o

como fator comum em evidência, temos:
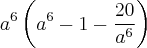
Recebeu a mensagem privada que lhe enviei?
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Marcones » Sáb Mar 21, 2015 23:41
por Marcones » Sáb Mar 21, 2015 23:41
Recebi sim!!
-
Marcones
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mar 21, 2015 11:10
- Formação Escolar: EJA
- Andamento: formado
 por Marcones » Dom Mar 22, 2015 14:47
por Marcones » Dom Mar 22, 2015 14:47
Eu gostaria de saber como faço pra chegar nesses respectivos resultados. Já tentei de tudo quando é modo que encontrei. São casos especiais? Por que?
Fatoração


-
Marcones
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Mar 21, 2015 11:10
- Formação Escolar: EJA
- Andamento: formado
 por Cleyson007 » Sex Mar 27, 2015 11:42
por Cleyson007 » Sex Mar 27, 2015 11:42
Olá, bom dia!
Desculpe a demora meu amigo..
É um caso especial sim! Estamos trabalhando com o produto e a soma!
É algo bem assim (para o exercício 43):
Temos que ter dois números que ao serem multiplicados resulte em -20. E, dois números que ao serem somados resulte em -1.
Basta montar um sistema de equações para os números em questão (a saber, x e y).
(x)(y) = -20
x + y = -1
Resolvendo o sistema acima encontramos -5 e 4.
Tem interesse na mensagem privada que lhe enviei?
Abraço e bons estudos

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fatoração Algébrica
 por Sasuke » Sáb Ago 23, 2014 22:09
por Sasuke » Sáb Ago 23, 2014 22:09
- 3 Respostas
- 2154 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 21:23
Álgebra Elementar
-
- Ajuda fatoração algébrica
por lucas7 » Ter Fev 15, 2011 19:53
- 10 Respostas
- 6715 Exibições
- Última mensagem por lucas7

Qui Fev 17, 2011 06:35
Álgebra Elementar
-
- [fração algébrica] fatoração
por Ederson_ederson » Sáb Jun 27, 2015 20:15
- 4 Respostas
- 3716 Exibições
- Última mensagem por Ederson_ederson

Qua Jul 08, 2015 11:27
Álgebra Elementar
-
- [Fatoração Algébrica] Conceito cubico e quadrado
por LucasMateusx » Ter Jan 03, 2017 13:42
- 1 Respostas
- 1930 Exibições
- Última mensagem por petras

Qui Jan 05, 2017 08:18
Álgebra Elementar
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8922 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 Lógico que sim!
Lógico que sim!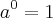 . Logo temos,
. Logo temos, 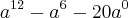 .
. como fator comum em evidência, temos:
como fator comum em evidência, temos: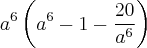







![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.