Nesse tipo de problema " ...então, sabendo que joão come 2 laranjas a cada semana, calcule a massa do Sol." a primeira coisa que você precisa fazer é equacionar o problema! Relacionar todas as variáveis do mesmo.
Pois bem, vamos analisar cada sentença.
LKSREIS escreveu:Uma empresa de táxi compra diariamente 560 L de combustível para abastecer sua frota.
Supondo que cada táxi use, por dia, do mesmo volume de gasolina

e que o número de táxis da frota é
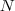
, então a primeira equação é
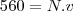
Agora:
LKSREIS escreveu:Em certo dia, dois táxis estavam quebrados e o combustível destinado a eles foi dividido igualmente entre os demais. Sabendo que neste dia cada táxi recebeu 5 L a mais, qual é a quantidade de táxis da frota?
Mesmo que os táxis tenham quebrado, a empresa não deixou de comprar os mesmo 560 litros de gasolina. Estes foram divididos entre os

táxis restantes que receberam, cada um,
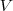
litros de gasolina. Como o produto de números de táxis com o volume diário de consumo de cada um é constante e igual a 560, então
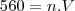
.
Mas, alem disso, sabemos que , nessa situação, o número de táxis reduziu-se de 2 e que o volume de gasolina diário de cada um aumentou de 5. Portanto,
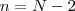
e
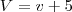
. Assim, a 2° equação é
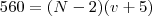
.
Pronto. Temos um sistema com 2 equações e duas variáveis. À princípio, ele deve ser solúvel.
Eu acredito q a solução é
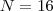
.


 e que o número de táxis da frota é
e que o número de táxis da frota é 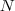 , então a primeira equação é
, então a primeira equação é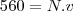
 táxis restantes que receberam, cada um,
táxis restantes que receberam, cada um, 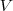 litros de gasolina. Como o produto de números de táxis com o volume diário de consumo de cada um é constante e igual a 560, então
litros de gasolina. Como o produto de números de táxis com o volume diário de consumo de cada um é constante e igual a 560, então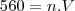 .
.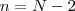 e
e 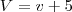 . Assim, a 2° equação é
. Assim, a 2° equação é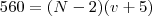 .
.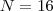 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.